
Взаимодействие уединенных волн в двухжидкостной магнитной гидродинамике…
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. Естественные науки. 2017. № 1
65
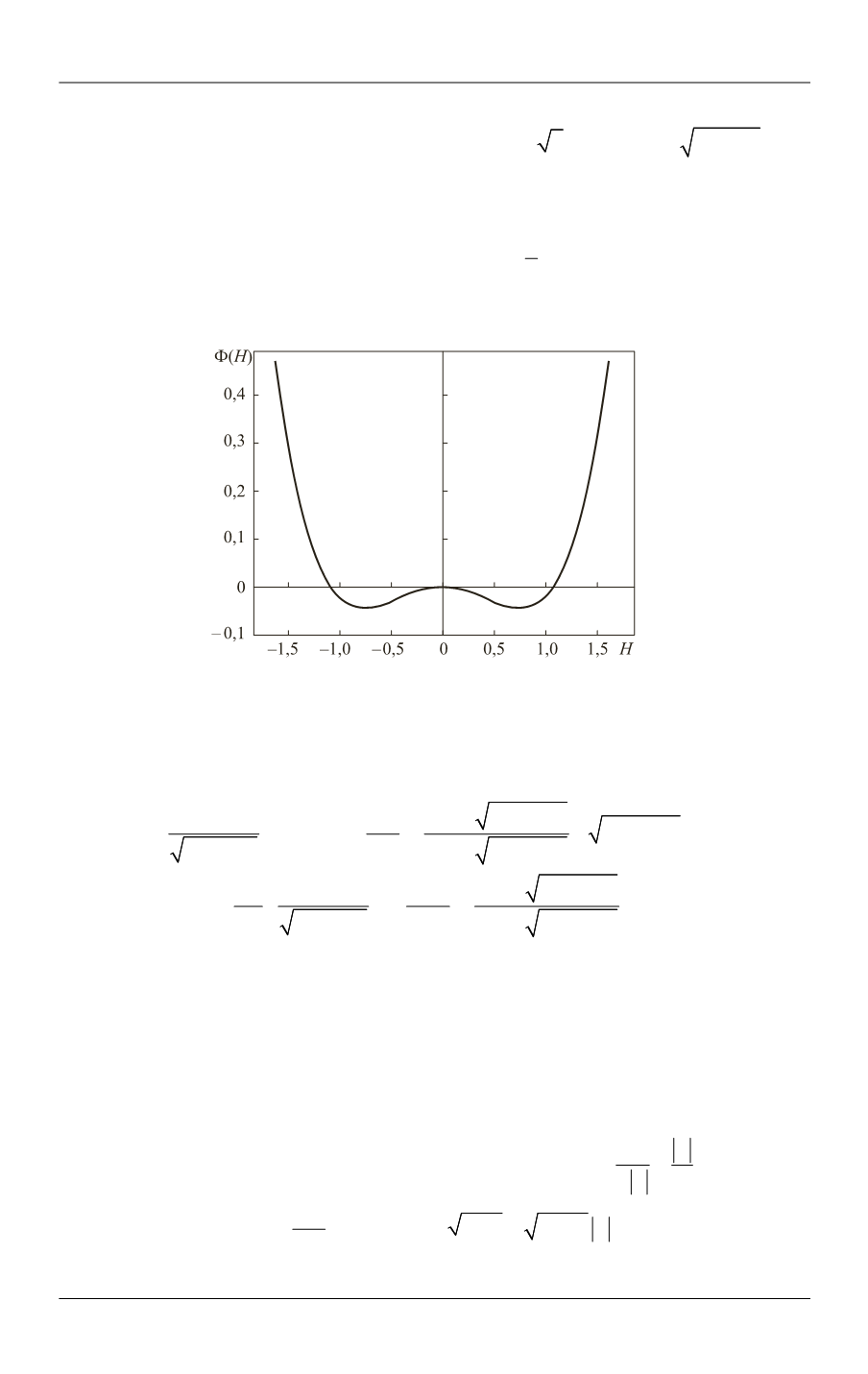
альная функция
( )
H
имеет вид, представленный на рис. 1. Для существования
уединенной волны требуется, чтобы
0
E
и
2
m
H
, где
2 2
2 1
m
H
b
. Та-
ким образом, приходим к следующим необходимым и достаточным условиям су-
ществования уединенной волны:
2
2
2 2
1
0,
0, 0
;
2
1
,
2 .
m
E
b H
(17)
Рис. 1.
Потенциальная функция
( )
H
2 2
(
0,7)
b
(14)
Формулы (15), (16) задают две полуограниченные дуги, аналитические вы-
ражения которых получают вычислением интегралов
(0
)
m
H H
2
2
2
2
2
2
2
2
2
2
2
(2 )
1
( )
2
ln
const;
2 ( )
( )
ln
const,
2
2
2 ( )
m m
m
m m m
m m
m m m
H
H H H
H
dH
H H
H
H
H H H
b dH
b H H H
H
H H
H H H
(18)
где константы определяются координатой горба
m
H H
уединенной волны и
фазой вектора
H
в горбе в начальный момент времени. По умолчанию, эти
величины полагают нулевыми и тогда постоянные в (18) также равны нулю.
Рассмотрим граничную задачу о возбуждении уединенной волны в покоя-
щейся плазме с плотностью
и с напряженностью магнитного поля
,
H H
бегущей вдоль магнитного поля. Для характерных масштабов имеем
2
2
0
2
0
0
,
,
,
;
2 2
4 4 ,
4
4
.
a D
u a J
u a D u a V
J
J
H D
a
D
















