
А.В. Хохлов
104
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. Естественные науки. 2017. № 3
Разрыва в точке
1
t t
=
нет, поскольку
(0) 0.
Π =
Хорошо заметна нелинейная
зависимость КП от
.
σ
При
[0, 6;1]
σ∈
на кривой обратной ползучести есть
участок выпуклости вверх и точка перегиба. При
1,1
σ >
КП обрывается еще на
первом участке (
1
t t
<
), так как нарушается условие
( )
t D
Φ
σΠ ∈
(при
( )
t
ε =
1);
+
= ω =
кривая синего цвета — КП при
1, 5,
σ =
штриховая линия красного цве-
та — кривая обратной ползучести для линейной модели Фойгта
( ( ) )
x x
Φ =
с
1,
σ =
штрихпунктирные линии —КП при постоянном напряжении (без разгрузки).
Кривые обратной ползучести (с
σ =
1,
=
1
10
t
) моделей, задаваемых МФ
Φ =
3
( ) ( / ) ,
x A x C
=
0, 5,
A
=
1
C
и тремя ФП вида (5) с
0,1:
λ =
ФП РеМ-3
(КП голубого цвета с
α =
0,
β =
1, 5,
γ =
0, 5
), РеМ-2 (КП синего цвета с
α =
0,1,
β =
0, 4
), СиМ-2 (КП красного цвета с
α =
0,
β = γ =
1, 5
) приведены на рис. 3,
б
.
Для МФ
−λ
Π = β − γ
( )
t
t
e
(РеМ-3 и СиМ-2),
γ∈ β
[0; ],
и
Φ =
( )
,
n
x Ax
>
0,
n
фор-
мула (12) дает
−λ −
−λ
ε = λ γ σ
− >
1
2 2
( )
( )
[
] 0
n n
t t
t n
t An
e
e
для всех
>
0,
n
т. е. кривые
обратной ползучести выпуклы вниз на луче
>
1
t t
(это верно и для МФ
Φ
,
рав-
ной линейной комбинации степенных функций с положительными коэффици-
ентами, в частности, (7)). Штриховыми линиями показаны кривые обратной
ползучести соответствующих линейных моделей (с
Φ =
( ) ),
x x
штрихпунктир-
ными — обычные КП (без разгрузки).
Свойства кривых ползучести для кусочно-постоянных программ нагруже-
ния.
Оператор (1), переводящий процесс
σ
( )
t
в
ϕ ε
( ( )),
t
линеен и инвариантен
относительно сдвигов по времени, поэтому он переводит программу нагружения с
n
ступеньками
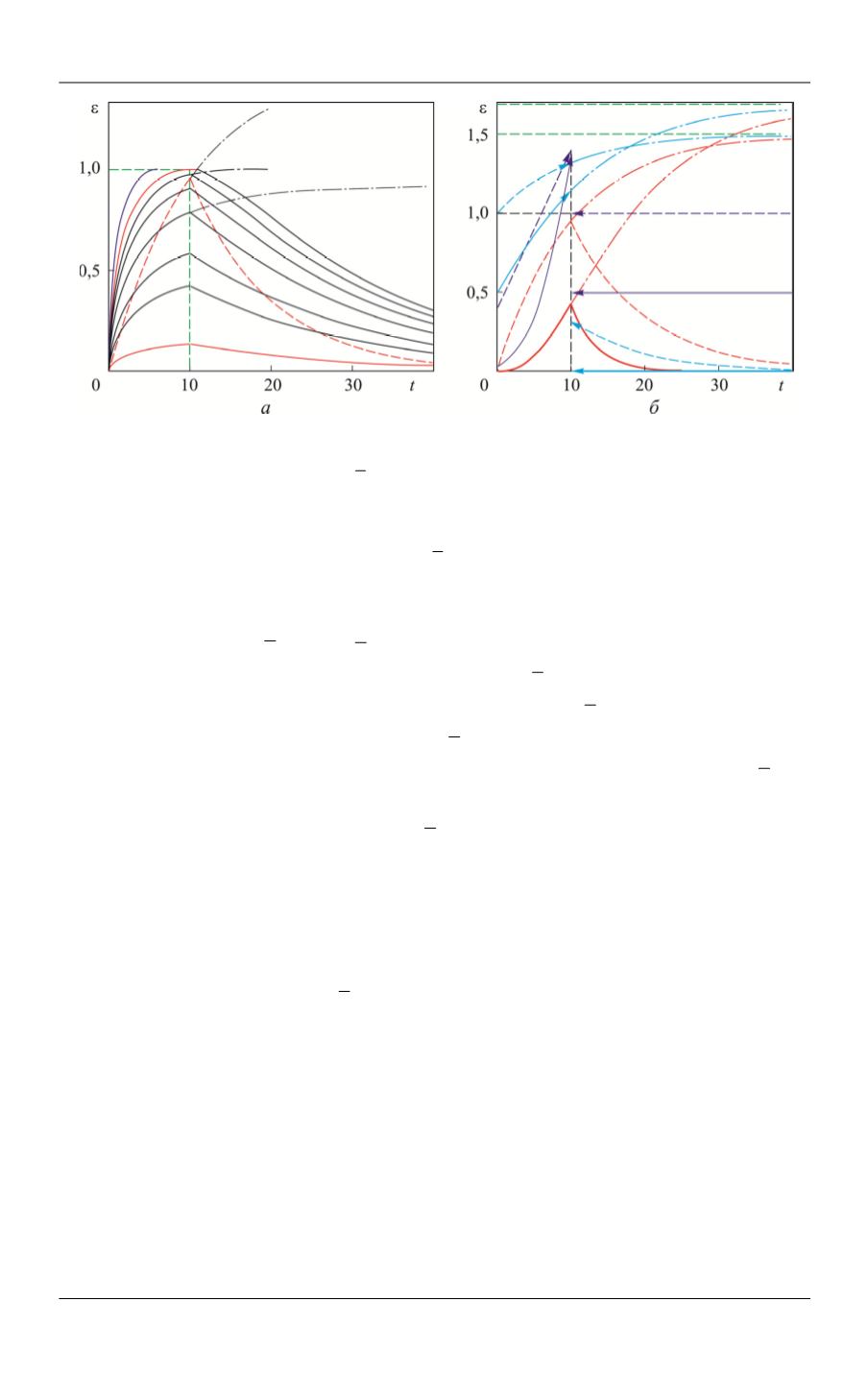
Рис. 3.
Кривые обратной ползучести (11) модели с
2 0,5
( ) [1 ( 1) ] ,
x
x
Φ = − −
∈
[0; 1],
x
и
,
t
e
−λ
Π = β −β
1,5,
β =
0,1,
λ =
при
σ =
0,01; 0,1; 0,2; 0,4; 0,6; 0,8; 1,0
(
а
) и шести моделей
с
3
0,5
x
Φ =
(сплошные линии) или
x
Φ =
(штриховые линии) в сочетании с функциями
ползучести РеМ-3 (голубые линии), РеМ-2 (синие линии) и СиМ-2 (красные линии) для
1
σ =
(
б
)
















