
Анализ общих свойств кривых ползучести при ступенчатых нагружениях…
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. Естественные науки. 2017. № 3
101
с
0, 5,
A
3
n
(сплошные КП),
3
( )
x Ax
(КП со стрелками) и
1/3
( )
x Ax
(штрихпунктирные КП). Все три КП для ФП РеМ-4 (ФП (5) с
1,
0, 5,
0, 02
) показаны черным цветом, для РеМ-3 (с
0,
1,
0, 5)
—
голубым цветом, для модели Максвелла (с
0,
0, 03,
1)
— синим цве-
том, для модели Фойгта (с
0,
1, 5))
— красным цветом, для степенной
ФП — желтым цветом. Примечательно, что КП модели Фойгта с МФ (10) имеет
две точки перегиба. У степенной ФП
(0) 0,
как и у модели Фойгта, но еще и
(0) ,
и у КП нет горизонтальной асимптоты (так как
( )
).
Поскольку
показатель степенной ФП
1 / 3,
u
КП для МФ
3
Ax
получается прямолиней-
ной, а КП для МФ (10) — очень близкой к прямолинейной. Штриховые кривые —
КП тех же линейных моделей (при
( )
x x
) с такими же значениями МП (для
сопоставления).
Зависимость КП двух нелинейных моделей от
,
полученных из РеМ-4 (ФП (5)
с
0,1,
0, 02,
1,
0, 5
) и степенной ФП
1/3
( )
/ 3
t t
введением МФ
(6), дающей для скорости ползучести зависимость
1
*
( )
(
)
V A
с
0, 5,
A
*
1, 5,
показана на рис. 2,
б
[51]. Для степенной ФП —
0, 5; 0, 8; 0, 9; 1, 0;
1,1; 1, 2; 1, 3; 1, 7
(КП желтого цвета), для ФП РеМ-4 —
0, 4; 0, 5; 0, 6; 0, 7;
0, 8; 0, 9; 1
(КП черного цвета); стрелками помечены КП с
1.
Поскольку
( )
x
из (6) обладает асимптотой
*
,
x
то КП
*
*
( )
ln[ / (
( ))]
t A
t
неограни-
ченно растут при
*
( )
/ ,
t
если только
*
/ ( ) (для указанных ФП это
выполнено при всех
0,
так как
( )
), т. е. каждая КП имеет вертикальную
асимптоту
*
( ),
t t
где
*
*
( )
/ .
t
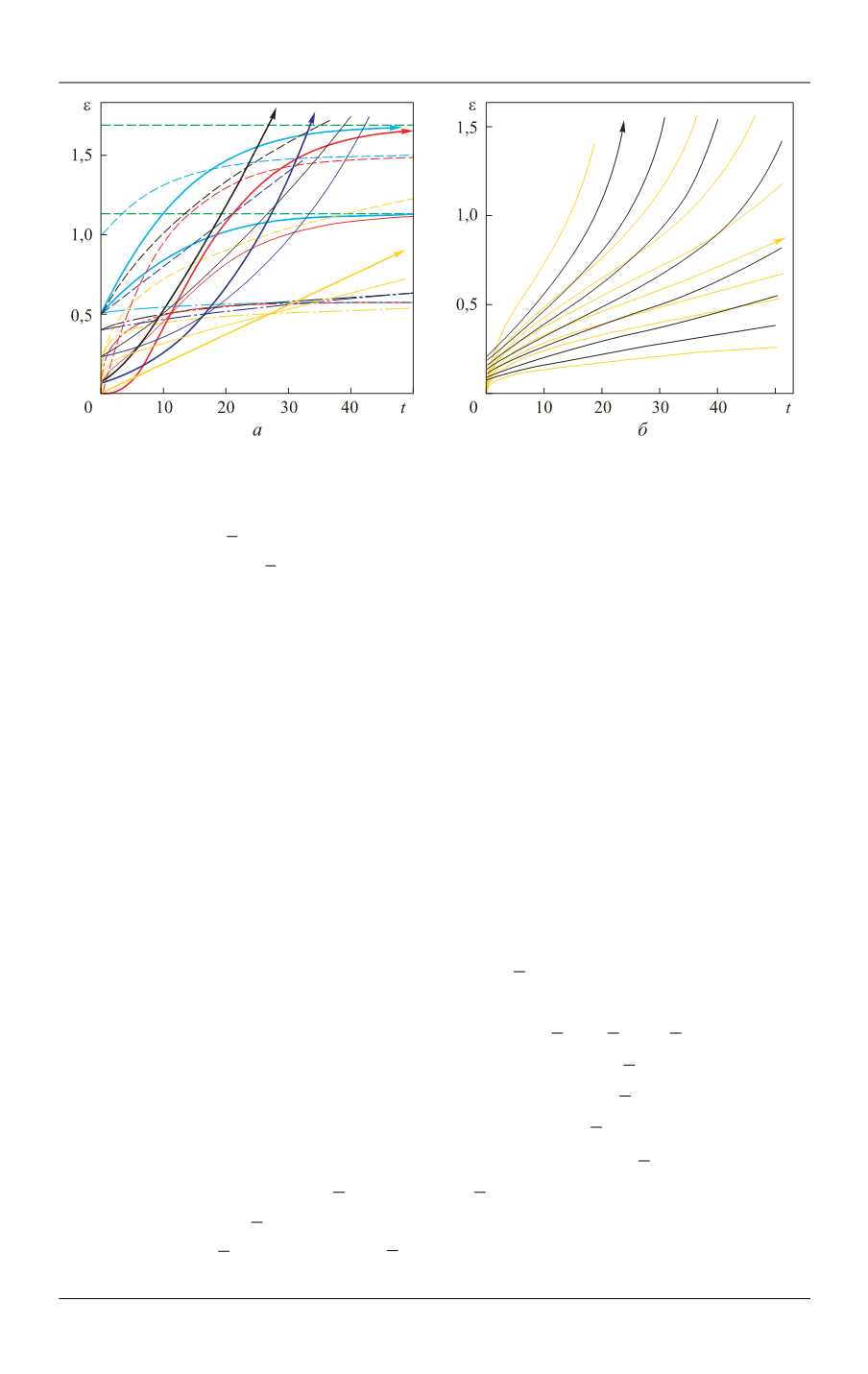
Рис. 2.
Кривые ползучести (9), порожденные ОС (1) для 15 пар материальных функций
(пяти видов
( )
t
и трех
( )),
x
иллюстрирующие разнообразие форм КП (
а
) кривые
ползучести двух нелинейных моделей (1) с материальной функцией (6) в сочетании с
ФП
1/3
/ 3
t
для
0,5; 0,8; 0,9; 1,0; 1,1; 1,2; 1,3; 1,7
(желтые КП) и с ФП вида (5) для
0,4; 0,5; 0,6; 0,7; 0,8; 0,9; 1,0
(черные КП) (
б
)
















