
Анализ общих свойств кривых ползучести при ступенчатых нагружениях…
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. Естественные науки. 2017. № 3
99
Кривые ползучести при постоянном напряжении.
Кривые ползучести ОС
(1) при мгновенном нагружении
σ = σ
( )
( ),
t
h t
σ >
0,
имеют вид
ε σ = Φ σΠ
( , )
( ( ))
t
t
при
σΠ <
( ) ,
t x
(9)
где
−
Φ = ϕ
1
:
,
= ϕ
: sup ( )
x
x
— верхняя грань области определения МФ
Φ
( ).
x
Семейство КП (9) возрастает по
σ
(так как
Φ
возрастает), а при любом
σ >
0 КП возрастает по
t
на всем промежутке, где
σΠ <
( ) .
t x
Если
x
= ∞
(как для линейного ОС, например), то
[ ; )
D x
Φ
= ∞
и КП определе-
ны при всех
0
σ >
и
0.
t
≥
Если
,
x
< ∞
то
( )
t D
Φ
σΠ ∈
только при
/ (0)
x
σ< Π
и
( ) / ;
t x
Π < σ
это означает, что КП существует только для напряжений
*
,
σ< σ
*
:
/ (0),
x
σ = Π
и обрывается в момент
*
,
t
удовлетворяющий уравнению
*
( ) / ,
t
x
Π = σ
если
/ ( )
x
σ > Π ∞
(если
Π ∞ < ∞
( )
КП с малым
σ
не обрывается).
Таким образом, если
< ∞
x
и
Π ≠
(0) 0,
то параметр
σ = Π =
*
:
/ (0)
x
E x
можно
трактовать как предел (мгновенной) прочности при растяжении, и в ОС (1) уже
встроен критерий разрушения. Если
( ) ,
x
Φ < ∞
т. е.
,
+
ω < ∞
разрушение при рас-
тяжении происходит по достижению критической деформации:
*
:
( )
x
+
ε = Φ = ω
(такой физический смысл можно придать параметру
+
ω
). Если
( )
x
Φ = ∞
(т. е.
+
ω = +∞
и
ϕ
( )
x
имеет горизонтальную асимптоту
=
y x
— как у МФ (6)), то
любая КП для
σ > Π ∞
/ ( )
x
имеет вертикальную асимптоту
=
*
,
t t
где
*
( / ),
t p x
= σ
( )
p x
— обратная функция к
Π
( )
t
(она определена на промежутке
Π Π ∞
(0); ( )
).
Если
Π ∞ < ∞
( )
и
σ< Π ∞
/ ( ),
x
то уравнение
Π = σ
( ) /
t x
решений не имеет, КП
определена при всех
≥
0.
t
Поэтому уравнение кривой длительной прочности при
растяжении:
= σ
*
( / ),
t p x
∞
< σ <
,
E x
E x
где
= Π
: 1/ (0),
E
∞
= Π ∞
: 1/ ( )
E
— мгно-
венный и длительный модули линейного ОС (2) [48, 50]. Легко убедиться, что из
ограничений, наложенных на ФП следует, что
σ
*
( )
t
убывает (как и эксперимен-
тальные кривые длительной прочности), выпукла вниз и
σ →∞
*
( )
t
при
∞
σ→
.
E x
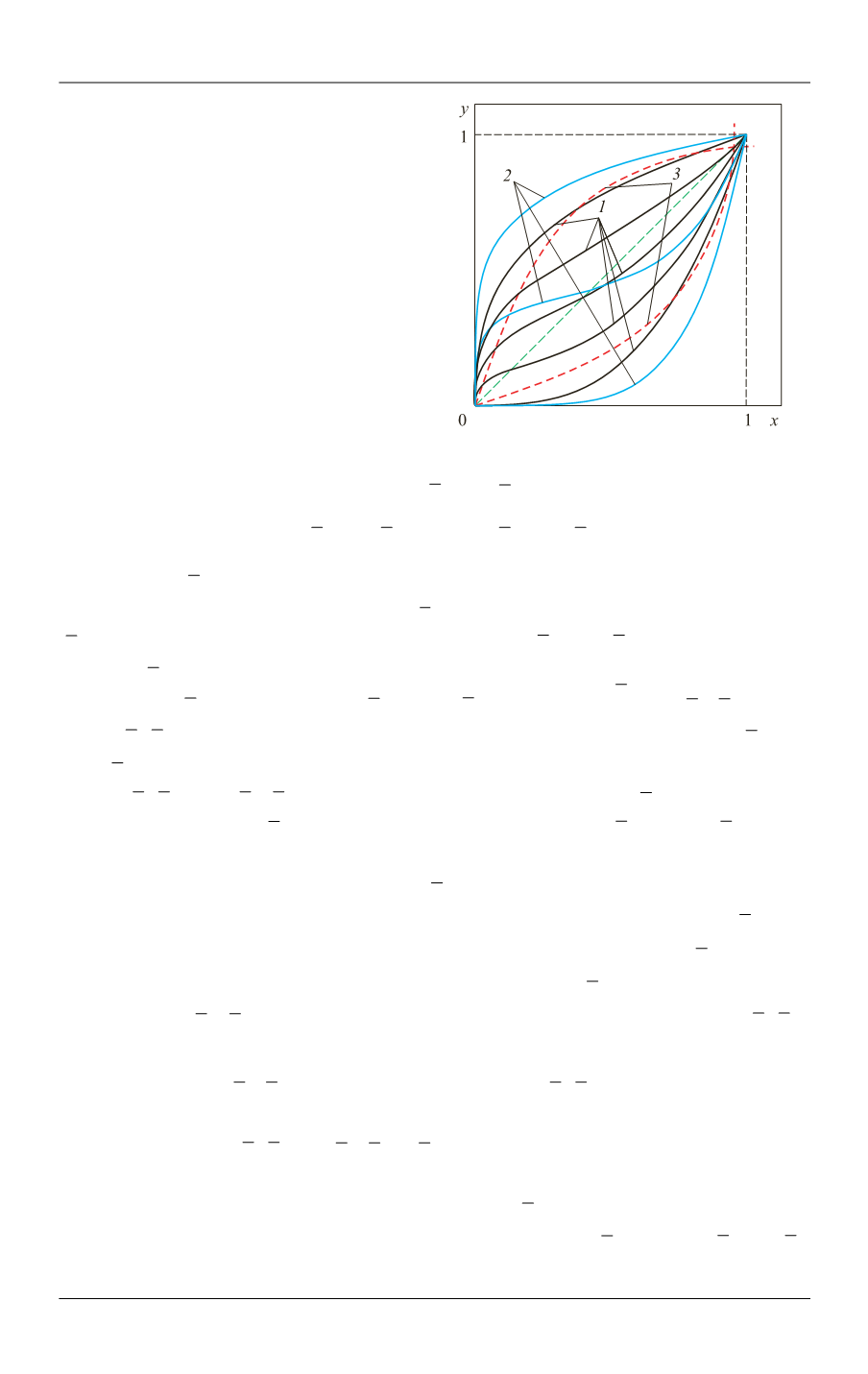
Рис. 1.
Графики функций (7) с
=
1 / ,
m n
=
3,
n
= =
1
A C
и
0; 0,25; 0,5; 0,75;
ϑ =
1 (
1
), графики при
=
5
n
и
0; 0,5; 1
ϑ =
(
2
)
и графики взаимно обратных МФ (6)
с
σ =
*
1,
=
0,3
A
(
3
)
















