Вариационная форма модели теплового пробоя твердого диэлектрика с зависящей от температуры теплопроводностью

12 / 15

Вариационная форма модели теплового пробоя твердого диэлектрика…
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. Естественные науки. 2017. № 5 15
тригонометрической и квадратичной ап-
проксимирующих функций при указанных
значениях *
1 B и *
2. B В первом случае в пра-
вой части этой формулы использовано зна-
чение *
1 75, 579,   а во втором — *
2  
76,755.  Поскольку 2 1 (1) > (1), q q аппрок-
симация функцией 2 ( )   действительного
распределения безразмерного потенциала
теплопроводности в плоском слое диэлек-
трика приводит к несколько большему зна-
чению *
2  по сравнению со значением *
1, 
полученным с использованием функции
1( ).  
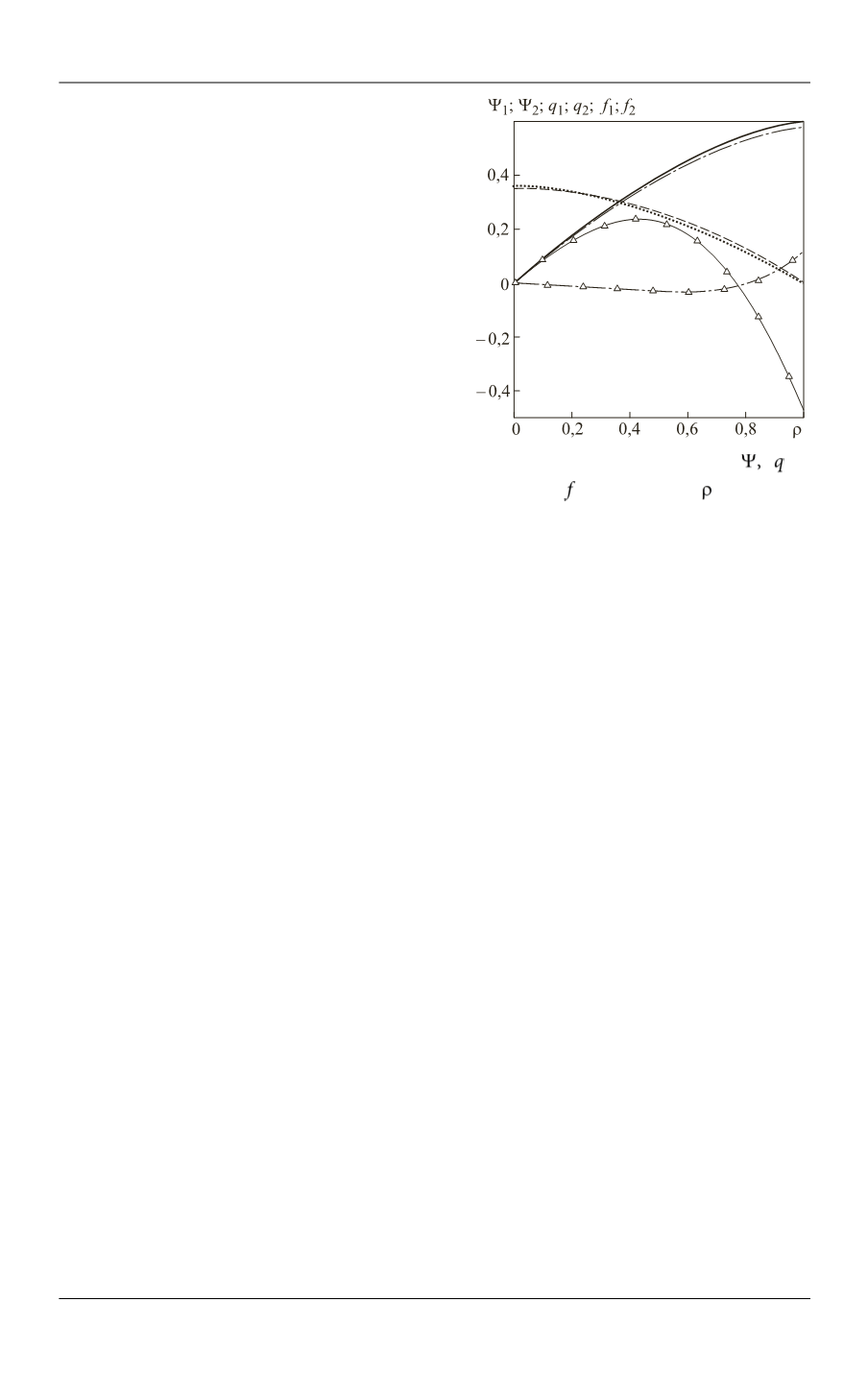
Штрихпунктирной и сплошной линия-
ми с треугольниками показаны зависимости
функций 
1( ) f и 
2 ( ). f Если действительное распределение безразмерной темпе-
ратуры в слое диэлектрика аппроксимировать функцией  2 ( ), то при одинако-
вых значениях  ординаты функции 
2( ) f по абсолютному значению более чем на
порядок превосходят ординаты функции 
1( ). f Ясно, что в этом случае целесооб-
разно отдать предпочтение аппроксимирующей функции  1( ) и из двух приве-
денных выше значений *
1 и *
2 принять первое более близким к истинному значе-
нию * . Результаты вычисления по формуле (18) дают значения     5
1 4, 298 10 и
    3
2 1, 504 10 , что также подтверждает сделанный вывод.
Заключение. Анализ стационарных точек функционала, входящего в вариа-
ционную форму математической модели теплового пробоя диэлектрика при
переменном напряжении, позволил установить связь между значением безраз-
мерного параметра ,  включающего напряжение пробоя, и характеристиками
слоя диэлектрика, теплопроводность материала которого зависит от температуры.
Из проведенного сравнения оценок интегральной погрешности для двух вариан-
тов функций (квадратичной и тригонометрической), аппроксимирующих дей-
ствительное распределение безразмерного потенциала теплопроводности в слое
диэлектрика, следует, что более близким к истинному экстремальному значению
 будет значение, полученное с использованием тригонометрической функции.
ЛИТЕРАТУРА
1. Сканави Г.И. Физика диэлектриков (область сильных полей). М.: Физматгиз, 1958. 908 с.
2. Борисова М.Э., Койков С.Н. Физика диэлектриков. Л.: Изд-во Ленингр. ун-та, 1979. 240 с.
3. Воробьев Г.А., Похолков Ю.П., Королев Ю.Д., Меркулов В.И. Физика диэлектриков (область
сильных полей). Томск: Изд-во ТПУ, 2003. 244 с.
4. Пробой диэлектриков // веб-сайт.
URL: (дата обращения: 20.11.2016).
Рис. 2. Зависимости функций и
от параметра