
Вариационная форма модели теплового пробоя твердого диэлектрика…
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. Естественные науки. 2017. № 5
11
зависимость
1
( )
B
при гипотетически выбранном значении
= 6
и значениях
= 1,167 (пунктирная линия), 0,2 (штрихпунктирная линия), 0 (сплошная линия);
−0,2 (штриховая линия), −1 (штриховая линия со светлыми треугольниками). При
= 0 кривая построена по формуле
1
1
2
1
1
0
=
exp
cos
,
8
1 cos( / 2)
2
B
d
B
которая следует из равенства (15) после предельного перехода при
0.
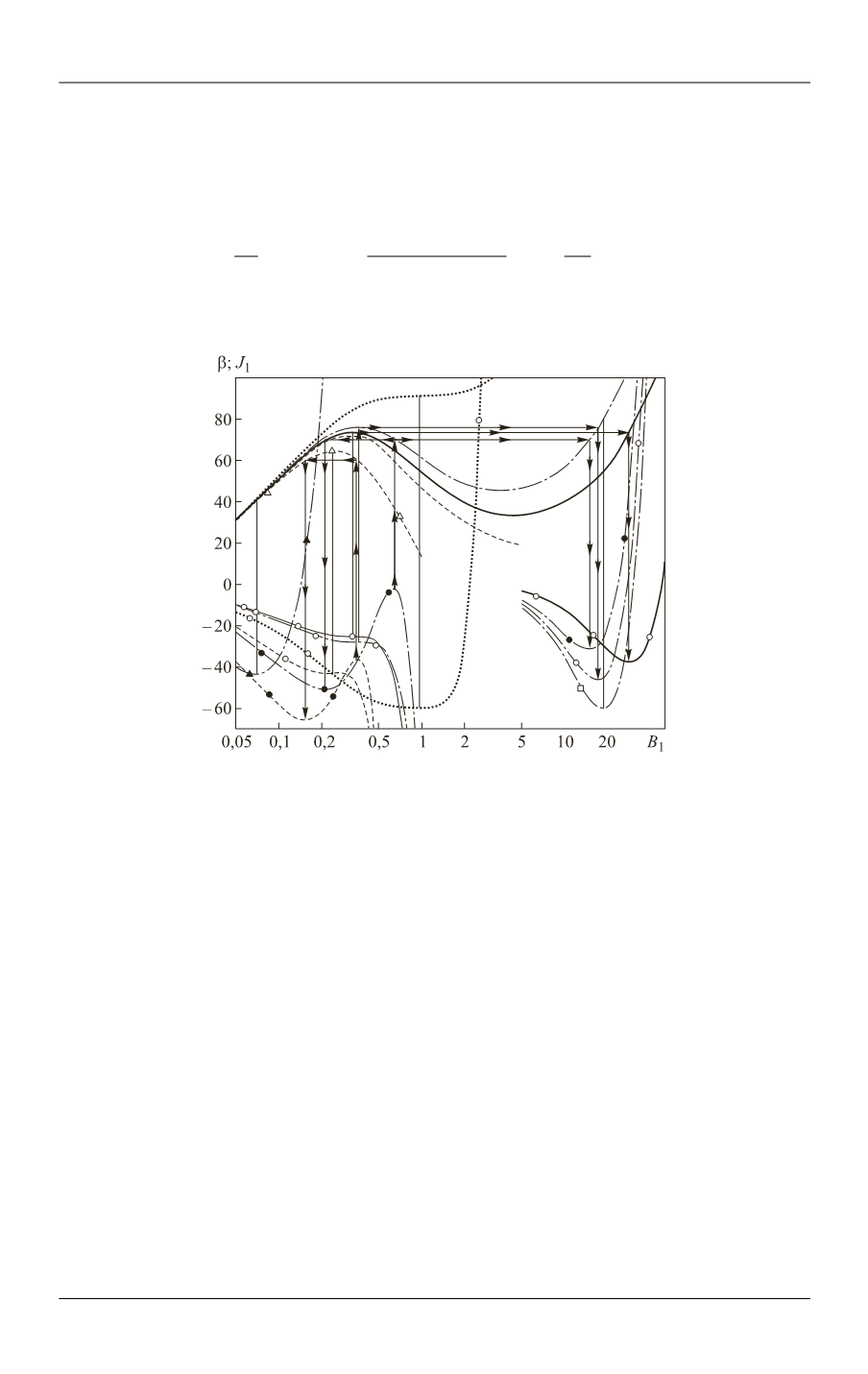
Рис. 1.
Зависимости параметра
и функционала
1
J
от коэффициента
1
B
при гипотетически выбранном значении
= 6
и различных значениях
В случае
= 0 зависимость
1
( )
B
достигает максимального значения
1
73, 393
при
1
0, 328
B
и минимального значения
33, 301
при
1
4, 406
B
(эти значения найдены из условия
1
/ = 0
B
с помощью метода безусловной
минимизации [18, 19] применительно к функции
2
1
1
( ) =( / )
F B
B
). При
= 0,2
значению
= 2
безразмерной температуры соответствует увеличение коэффици-
ента теплопроводности по сравнению с
*
в
exp(0, 2) 1, 221
раза. В этом случае
зависимость
1
( )
B
также имеет два экстремума: максимум с ординатой
*
1
75, 579
и абсциссой
*
1
0, 356;
B
минимум с ординатой
1
45, 037
и абсцис-
сой
1
3, 597
B
(эти значения также определены путем решения упомянутой выше
задачи безусловной минимизации). По мере возрастания параметра
происхо-
дит сближение экстремальных точек на зависимости
1
( )
B
и при
1,167
наступает объединение этих точек в точку перегиба с касательной, параллельной
оси абсцисс (см. рис. 1). При
>
зависимость
1
( )
B
является строго возрас-
тающей.
















