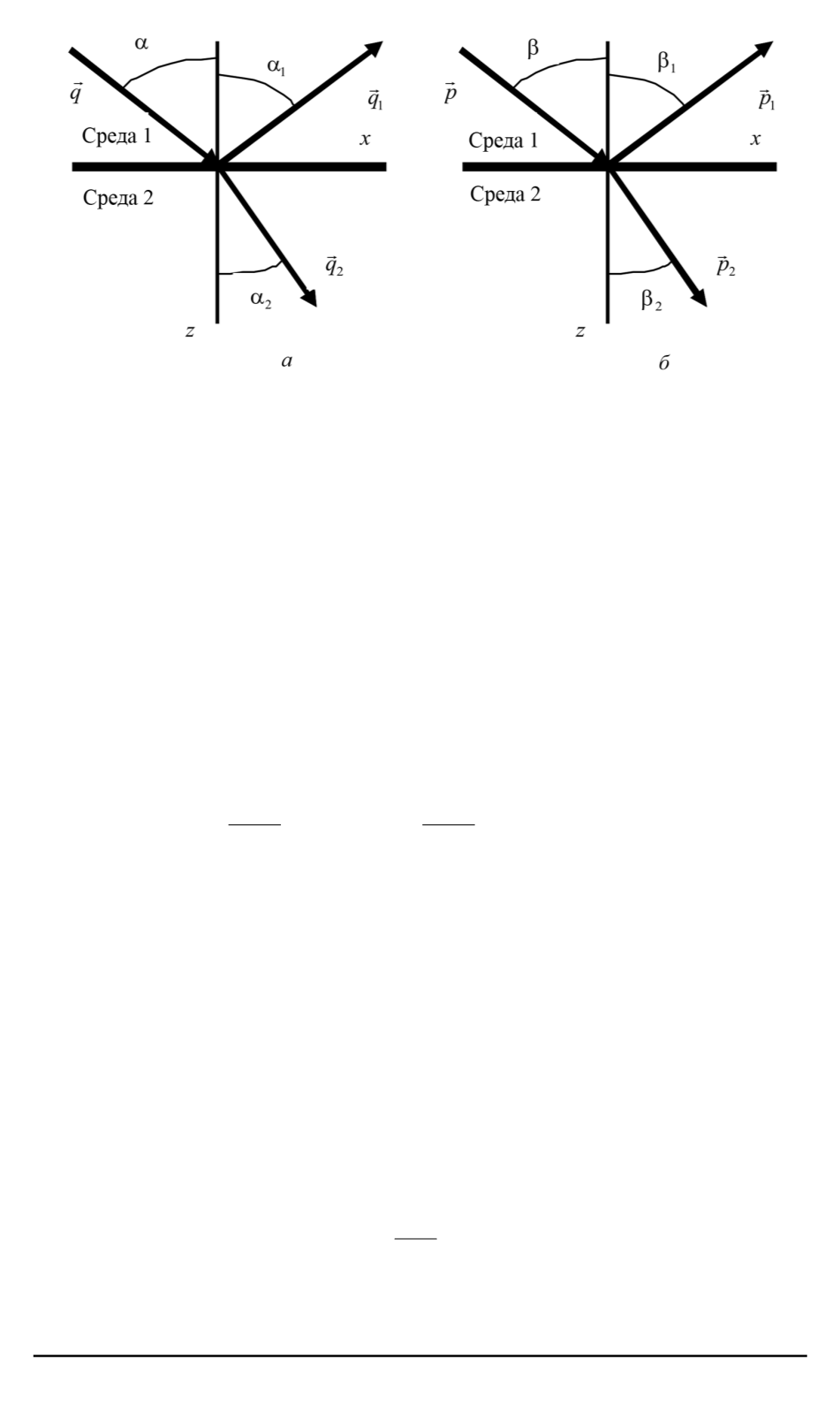
Рис. 1. Пространственная ориентация векторов
~
q
(
а
) и
~
p
(
б
)
Примем (по условию), что падающая волна однородна:
p
= 0
.
Соотношение
k
y
=
k
1
y
=
k
2
y
можно удовлетворить, если пра-
вильно выбрать систему декартовых координат:
k
y
= 0
. Отметим, что
должны быть выполнены следующие условия:
q
sin
α
=
q
1
sin
α
1
=
q
2
sin
α
2
;
0 =
p
1
sin
β
1
=
p
2
sin
β
2
.
(5)
Предположим, что
p
1
6
= 0
, тогда справедливы дисперсионные уравне-
ния
q
2
=
n
2
1
ω
2
c
2
;
q
2
1
−
p
2
1
=
n
2
1
ω
2
c
2
;
q
1
p
1
cos
ψ
1
= 0
.
Согласно условиям (5),
sin
β
1
= 0
, вектор
~p
1
параллелен оси
z
, при
этом векторы
~q
1
и
~p
1
взаимно ортогональны, следовательно, вектор
~q
1
параллелен оси
x
, т.е.
sin
α
1
= 1
. В этом случае
−
p
2
1
=
q
2
(1
−
sin
2
α
)
>
0
.
Поскольку величина
~p
1
определена как действительная векторная ве-
личина, полученный результат позволяет сделать вывод, что отражен-
ная волна не может быть неоднородной
p
1
= 0
.
Если отраженная волна однородна, то
q
1
=
q
=
n
1
ω
c
;
α
1
=
α,
т.е. модули волновых векторов падающей и отраженной волн одина-
ковы, а угол падения равен углу отражения.
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2013. № 3
21


