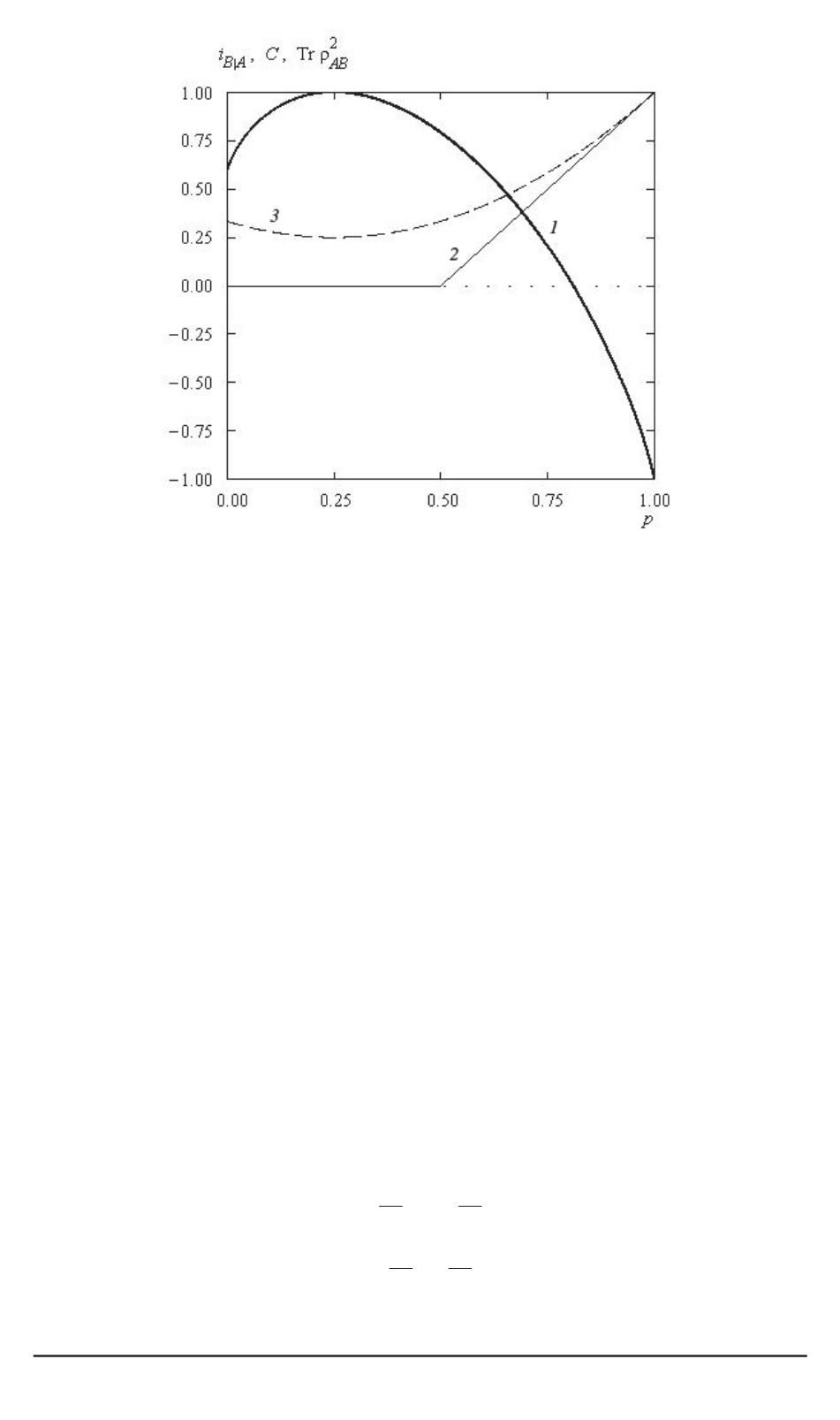
Рис. 6. Зависимость
i
B
|
A
(
1
),
C
(
2
) и Tr
ρ
2
AB
(
3
) от
p
=
p
4
исходного белловского
диагонального состояния (37)
достигая 1 при равенстве всех
p
i
. Но более важно, что имеется интер-
вал
0
,
5
< p <
0
,
81
, г де
i
B
|
A
>
0
и
С
>
0
. На этом интервале система
запутана, несмотря на энтропийную классичность.
Теперь рассмотрим диссипацию состояния (37) в присутствии об-
щего термостата. Известно, что вопреки ранее принятым взглядам
диссипация может не сводиться к декогеренции, а, напротив, играть
конструктивную роль в возникновении запутанности [29–36]. Следуя
работе [34], положим, что кубиты представляют двухуровенные ато-
мы, расположенные близко по сравнению с длиной волны. Диссипа-
ция происходит за счет спонтанной эмиссии фотонов, которые име-
ют существенную вероятность поглотиться соседним атомом. В [34]
решается уравнение динамики матрицы плотности и подробно анали-
зируются асимптотические решения
t
→ ∞
для различных исходных
состояний. В частности, асимптотическая матрица плотности при ис-
ходном состоянии (37) имеет вид
ρ
as
AB
=
⎛
⎜⎜⎜⎜⎜⎜⎜⎝
0 0 0
0
0
p
4
2
−
p
4
2
0
0
−
p
4
2
p
4
2
0
0 0 0 1
−
p
4
⎞
⎟⎟⎟⎟⎟⎟⎟⎠
.
(41)
48
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2010. № 3


