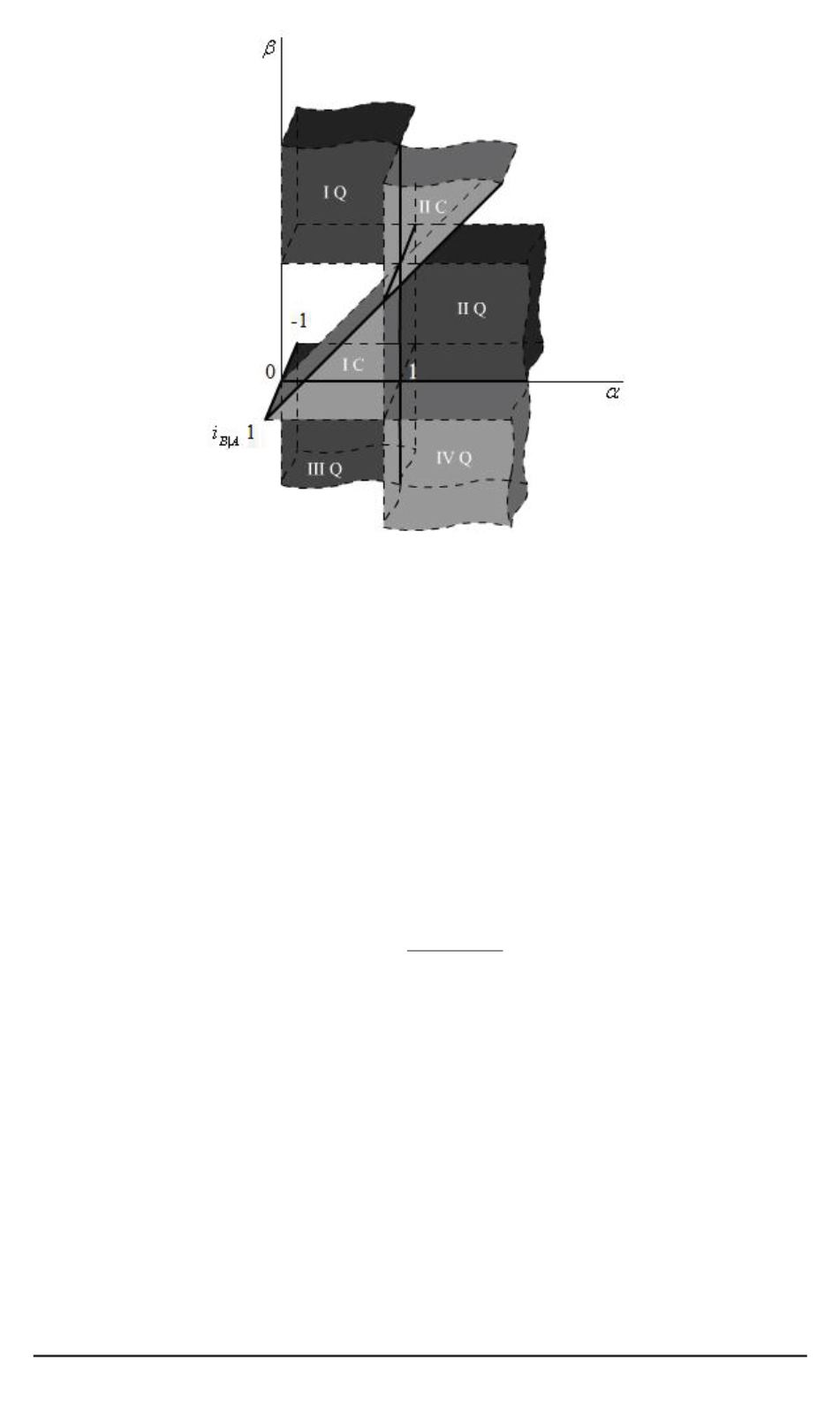
Рис. 2. Квантовая энтропийная диаграмма
I C,
0
α
1
,
0
β
1
,
0
i
B
|
A
1
,
0
γ
1
,
c
2
>
0
;
II C,
1
α
∞
,
1
β
∞
,
0
i
B
|
A
1
,
1
γ
∞
,
c
2
<
0
;
IQ,
0
α
1
,
1
β
∞
,
−
1
i
B
|
A
0
,
1
γ
∞
,
c
2
>
0
;
IIQ,
1
α
∞
,
0
β
1
,
−
1
i
B
|
A
0
,
0
γ
1
c
2
<
0
;
IIIQ,
0
α
1
,
−∞
β
0
,
−
1
i
B
|
A
0
,
−∞
γ
0
,
c
2
>
0
;
IVQ,
1
α
∞
,
−∞
β
0
,
0
i
B
|
A
1
,
−∞
γ
0
,
c
2
<
0
.
На трехмерной диаграмме рис. 2 трудно, однако, точно показать
границы разрешенных областей. Для их указания воспользуемся тем,
что (легко проверить) функцию независимости
i
B
|
A
можно предста-
вить в виде
i
B
|
A
=
β
(
α
−
1)
α
(
β
−
1)
.
(16)
В областях IC, IIC и IVQ
0
i
B
|
A
1
, что, согласно (16), при-
водит к системе двух неравенств относительно
α, β
. Их решения в
виде сечений
i
B
|
A
=
const показаны на рис. 3,
а
. Разрешенные обла-
сти примыкают к граничным плоскостям. В областях IQ, IIQ и IIIQ
−
1
i
B
|
A
0
. Решения соответствующей пары неравенств показа-
ны на рис. 3,
б
. Разрешенные области отделены от части граничных
плоскостей гиперболическими поверхностями.
На квантовом уровне величина
γ
недостаточна для различия при-
чин и следствий. Но пользуясь соответствием
c
2
и
γ
в обеих класси-
ческих областях и необходимым условием выполнения 7-й теоремы
Шеннона во всех шести областях (
c
2
>
0
⇒
α <
1
,
c
2
<
0
⇒
α >
1
),
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2010. № 3
41


