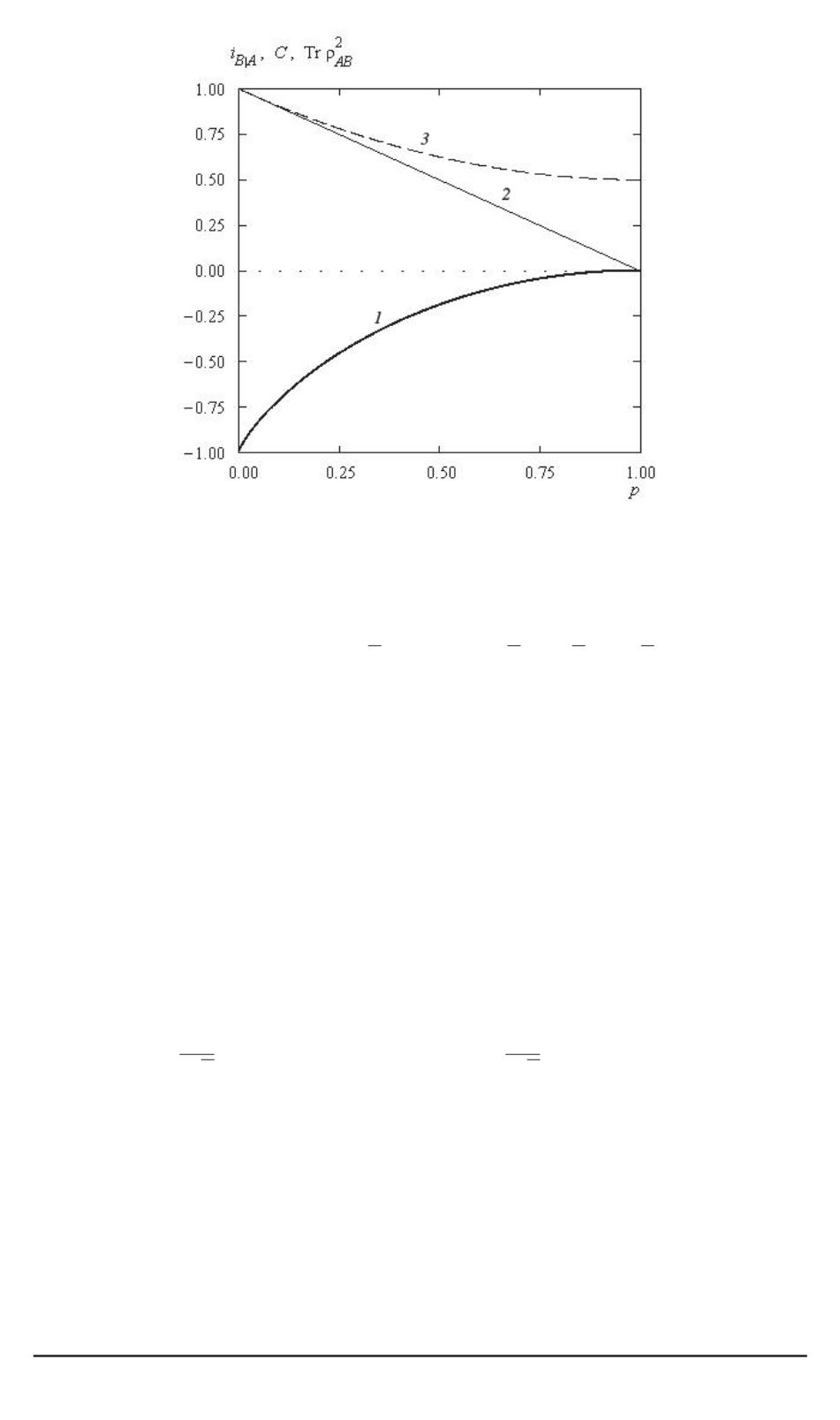
Рис. 5. Зависимость
i
B
|
A
(
1
),
C
(
2
) и Tr
ρ
2
AB
(
3
) от степени дефазирования
p
состояния (26)
Вновь справедливы соотношения (28), (30) и (31), но
S
(
AB
) =
−
1
−
p
2
log
2
1
−
p
2
−
p
2
log
2
p
2
;
(35)
С
= 1
−
p.
(36)
Поэтому при полном дефазировании
i
B
|
A
= 0
, т.е. подсистемы оста-
ются классически максимально коррелированными. При частичном
дефазировании
С
и отрицательная
i
B
|
A
являются равноправными ха-
рактеристиками квантовой коррелированности (рис. 5).
4.6. Белловские диагональные состояния.
Исходные белловские
диагональные состояния определяются как
ρ
AB
=
p
1
|
Φ
+
><
Φ
+
|
+
p
2
|
Φ
−
><
Φ
−
|
+
p
3
|
Ψ
+
><
Ψ
+
|
+
p
4
|
Ψ
−
><
Ψ
−
|
,
(37)
где
|
Φ
±
>
=
1
√
2
(
|
00
>
±|
11
>
);
|
Ψ
±
>
=
1
√
2
(
|
10
>
±|
01
>
)
.
(38)
По-прежнему справедливы (28), (30) и (31), но
S
(
AB
) =
−
4
i
=1
p
i
log
2
p
i
;
(39)
C
= max(2 max
{
p
i
} −
1
,
0)
.
(40)
Поведение
i
B
|
A
,
С
и Tr
ρ
2
AB
при выборе
p
4
=
p
,
p
1
=
p
2
=
p
3
= (1
−
p
)
/
3
показано на рис. 6. Видно, что
i
B
|
A
отражает смешанность состояния,
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2010. № 3
47


