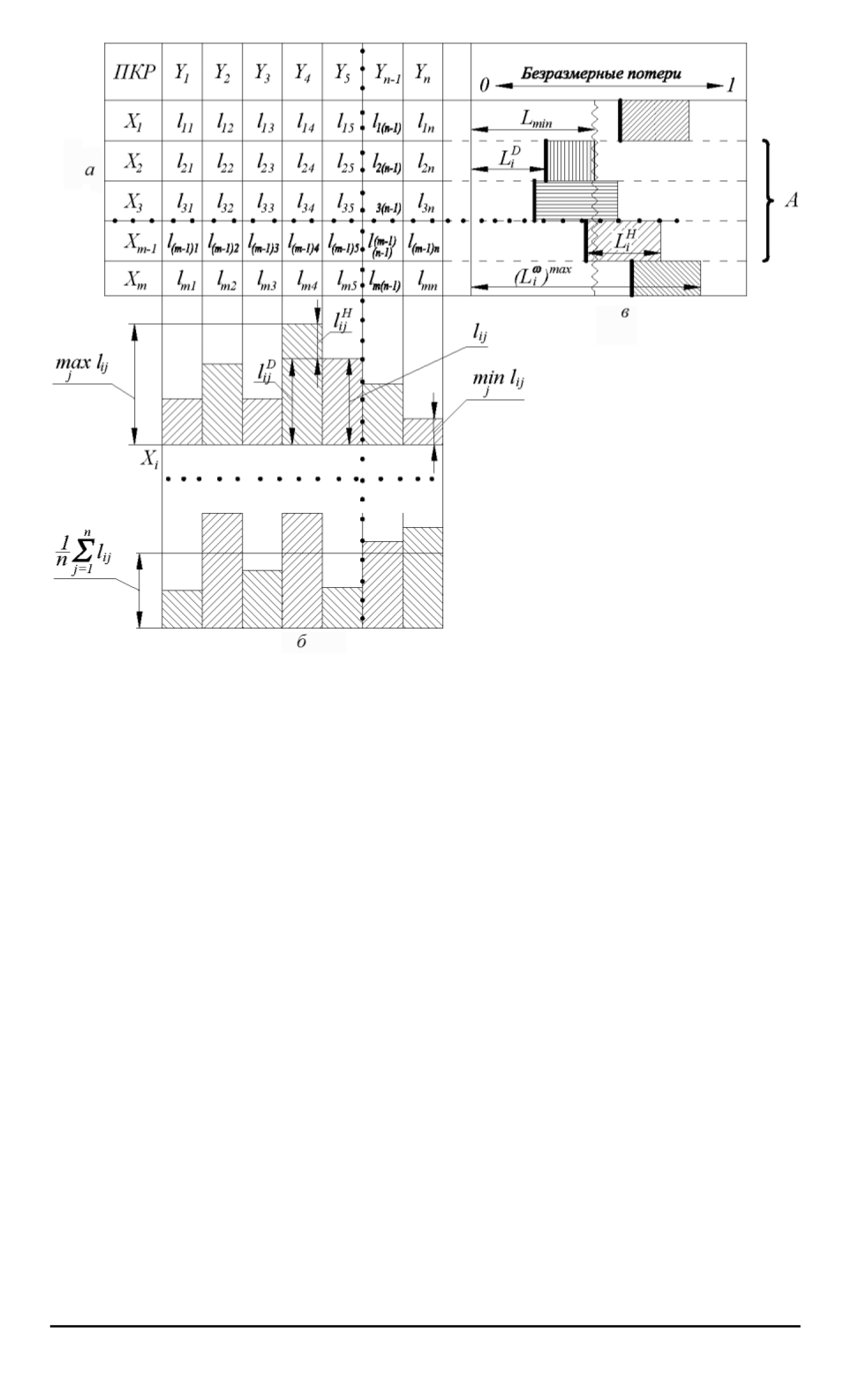
Рис. 2. Нечеткий выбор рационального варианта отбора абитуриентов:
а
— матрица потерь;
б
— гистограмма рассогласований;
в
— выделение множества
эффективных решений (
0
6
i
6
m
,
0
6
j
6
n
)
на рис. 2,
в
случае, таких решений три. Формально условие, выделяю-
щее эффективные решения, записывается в виде
(
L
ω
i
)
min
6
L
min
= min
i
(
L
ω
i
)
max
,
(8)
где
(
L
ω
i
)
min
— минимальное значение
i
-х суммарных потерь;
(
L
ω
i
)
min
=
=
L
D
i
.
Значение
L
min
— определяет положение волнистой линии на
рис. 2,
в
, которая в свою очередь определяет верхнюю границу сум-
марных потерь, т.е. если минимальное значение потерь
(
L
ω
i
)
min
будет
больше
L
min
, то такие варианты отбора исключаются из рассмотрения.
Детерминированная составляющая потерь
L
D
i
всегда остается
постоянной, а неопределенная составляющая лежит в диапазоне
0
6
L
H
i
6
L
H
i
max
, поэтому так как
L
ω
i
=
L
D
i
+
L
H
i
, то минималь-
ное значение
i
-х суммарных потерь
(
L
ω
i
)
min
=
L
D
i
, а максимальное
значение
(
L
ω
i
)
max
=
L
D
i
+
L
H
i
max
.
Пример 1.
Ниже приведен абстрактный пример анализа различ-
ных вариантов отбора, который в равной мере может относиться как к
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2007. № 3
111


