= +
∞
. Итак, при
ν
2
< ν
3
≤
ν
1
мы получаем тривиальное семей-
ство локализующих множеств
Ω
q
=
R
3
,
q <
−
1
, а при
ν
2
< ν
1
< ν
3
семейство локализующих множеств имеет вид
Ω
q
: (
q
+ 1)
x
2
+
qy
2
+
z
−
β
(2
q
+ 1)
2
≤
ρ
3
β
2
(2
q
+ 1)
2
,
(26)
где
ρ
3
=
τ
1
, ν
1
≥
ν
3
2
;
1
, ν
1
<
ν
3
2
.
С помощью соотношений (20) получаем неравенства, описываю-
щие пересечение
Ω
(
−∞
,
−
1)
семейства (26):
y
2
≥
(
g
2
(
ρ
3
, x, z
)
,
x
2
+ (
z
−
β
)
2
≤
(4
−
3
ρ
3
)
β
2
;
(
z
+
β
)
2
−
ρ
3
β
2
, x
2
+ (
z
−
β
)
2
>
(4
−
3
ρ
3
)
β
2
,
(27)
где
g
2
(
ρ
3
, x, z
) = 4
β
2
(
ρ
3
−
1)
−
x
2
+4
βz
−
4
β
p
(
ρ
3
−
1)[
ρ
3
β
2
−
x
2
−
(
z
−
β
)
2
]
.
Итоговые результаты.
Были рассмотрены пять промежутков из-
менения параметра: 1)
q >
0
; 2)
q
= 0
, 3)
−
1
< q <
0
, 4)
q
=
−
1
,
5)
q <
−
1
. Для каждого из этих промежутков получено локализующее
множество, в которое попадают все инвариантные компактные множе-
ства ПРТ-системы. Окончательный результат — это пересечение всех
полученных локализующих множеств, которое естественно описать в
виде системы неравенств. Однако вид этих неравенств зависит от соот-
ношений между параметрами
ν
1
,
ν
2
,
ν
3
. Разделим трехмерную область
изменения параметров
ν
1
,
ν
2
,
ν
3
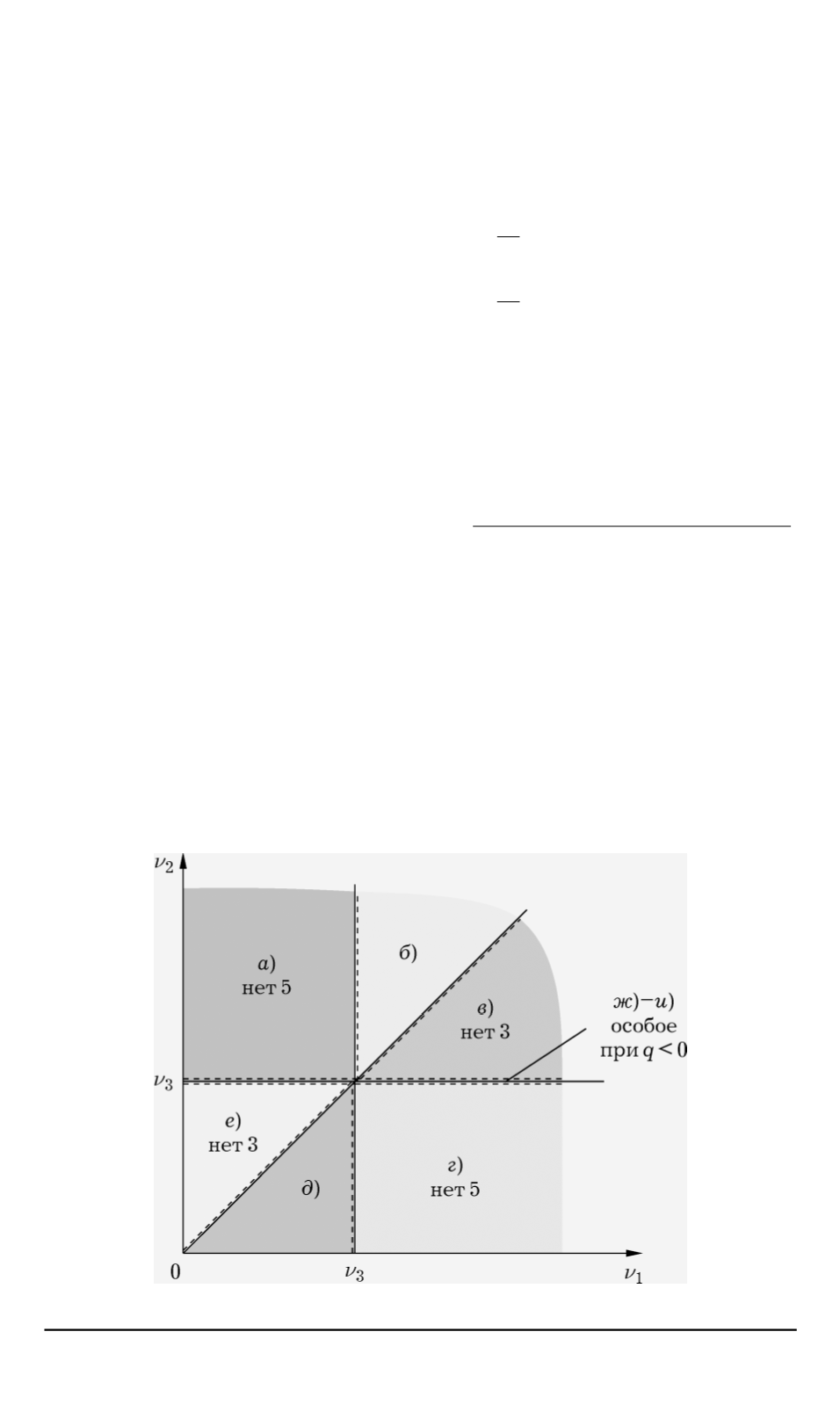
на несколько подобластей (рис. 1):
Рис. 1. Область изменения параметров системы
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2007. № 1
13


