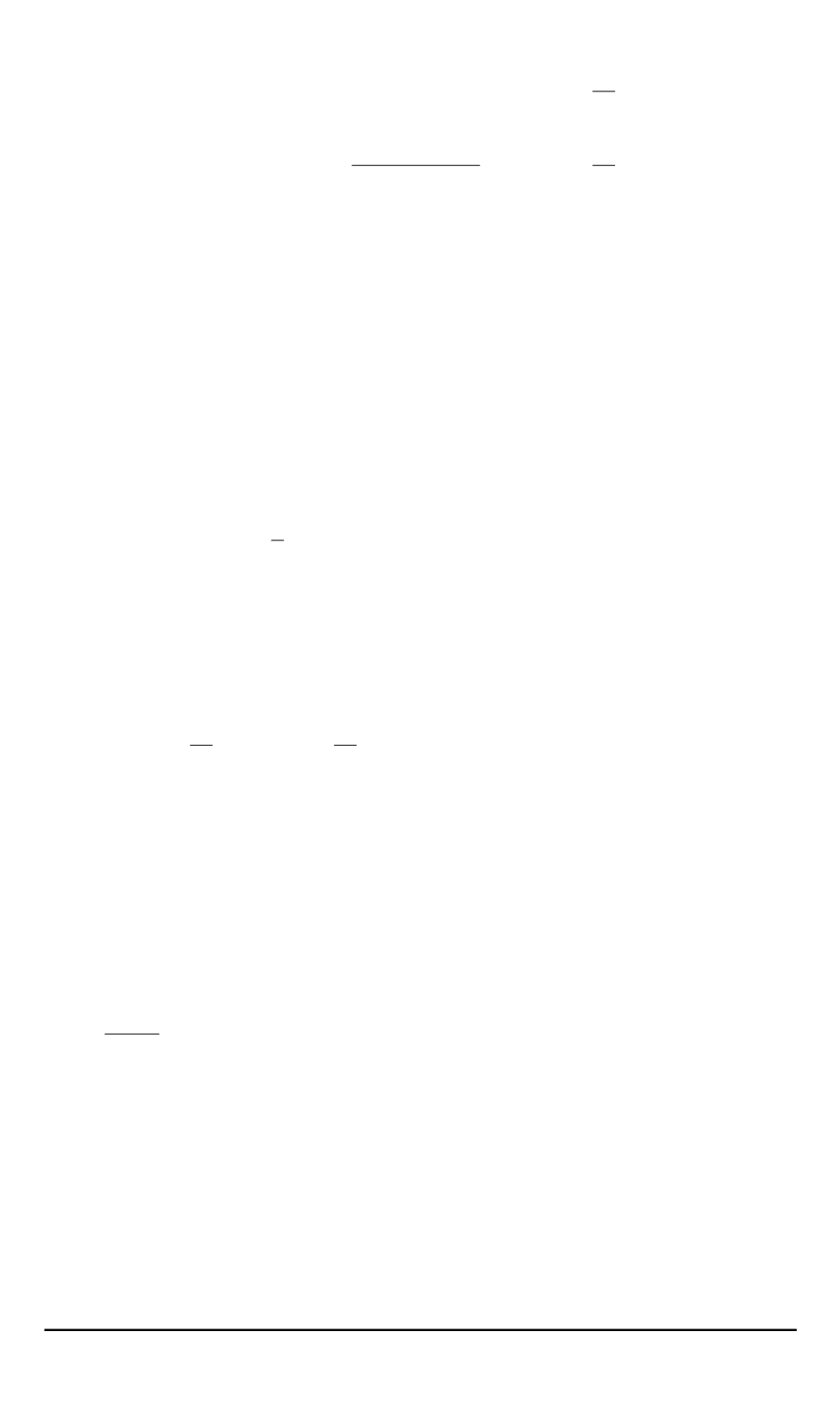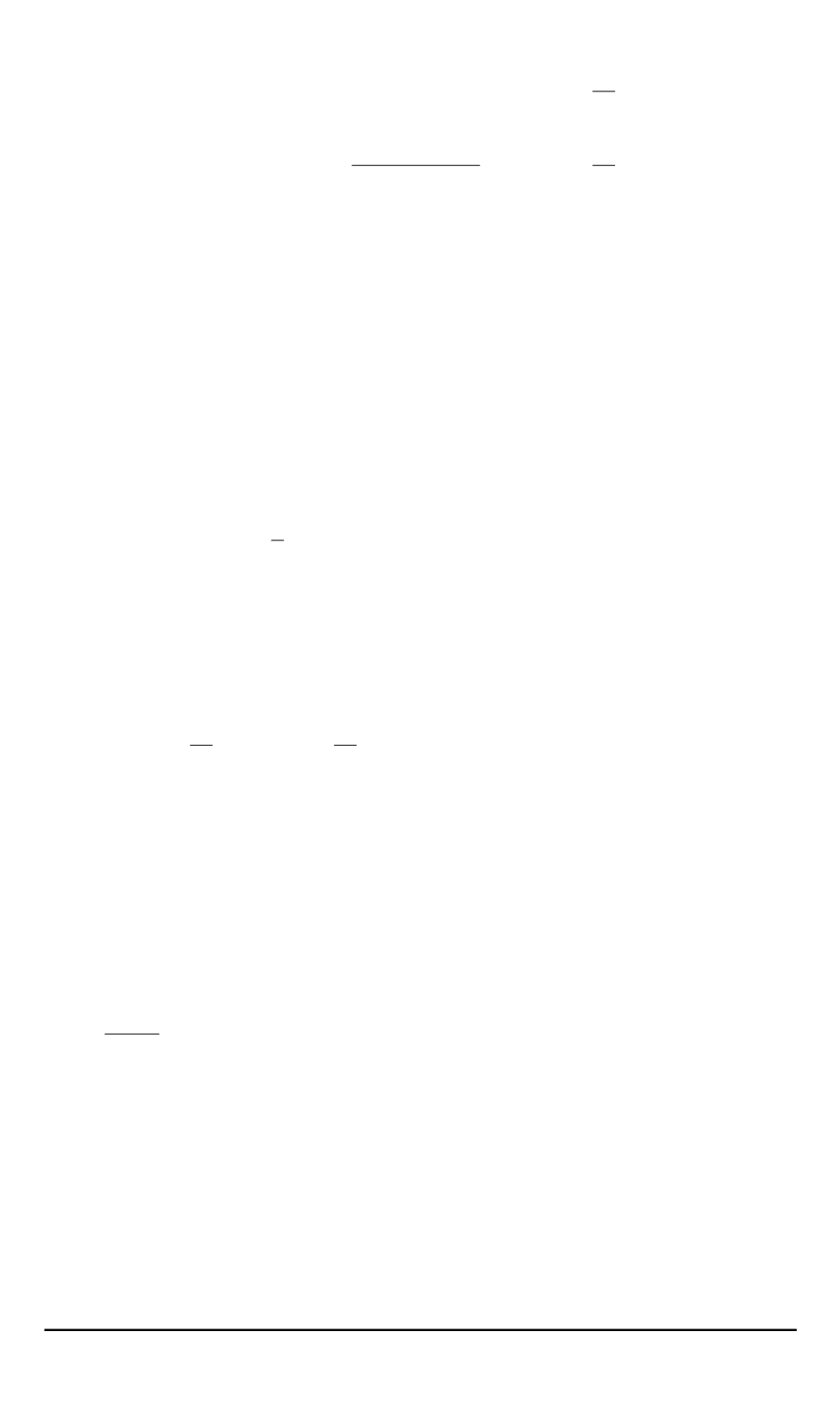
где
ρ
0
=
1
,
ν
1
≥
ν
3
2
;
τ
1
=
ν
2
3
4(
ν
3
−
ν
1
)
ν
1
,
ν
1
<
ν
3
2
.
Итак, при
q
= 0
получаем локализующее множество
Ω
0
, описыва-
емое неравенством
Ω
0
:
x
2
+ (
z
−
β
)
2
≤
ρ
0
β
2
,
(3)
что совпадает с неравенством (1) при
q
= 0
и
ρ
=
ρ
0
.
Локализующие множества в случае
−
1
< q <
0
.
При
q <
0
урав-
нение связи дает неограниченную поверхность, и непосредственно
использовать метод Лагранжа нельзя. Здесь удобно свести задачу к
двумерной, исключив переменную
y
с помощью уравнения связи. Из
уравнения связи находим
ν
2
y
2
=
1
q
ν
3
γ
2
−
ν
3
(
z
−
γ
)
2
−
(
q
+ 1)
ν
1
x
2
.
Исключив эту переменную из выражения для функции
p
, приходим к
задаче определения точных верхней и нижней граней функции двух
переменных:
p
(
x, z
) = (
q
+ 1)
μ
1
x
2
+
μ
3
z
2
−
2
γ
(1 +
μ
3
)
z
+ 4
γ
2
,
(4)
где
μ
1
= 1
−
ν
1
ν
2
,
μ
3
= 1
−
ν
3
ν
2
— промежуточные параметры, меньшие
единицы, на множестве
G
q
: (
q
+ 1)
ν
1
x
2
+
ν
3
(
z
−
γ
)
2
≥
ν
3
γ
2
.
(5)
При
−
1
< q <
0
множество
G
q
представляет собой внешность
эллипса. При
q
=
−
1
задача становится одномерной: требуется найти
экстремальные значения функции
p
(
x, z
) =
μ
3
z
2
−
2
γ
(1 +
μ
3
)
z
+ 4
γ
2
на множестве
G
−
1
:
|
z
−
γ
| ≥
γ
. При
q <
−
1
множество
G
p
ограничено
гиперболой. Рассмотрим эти случаи отдельно.
Считая, что
−
1
< q <
0
, выполним замену переменных
X
=
=
x
√
q
+ 1
,
Z
=
z
−
γ
. Тогда задача сводится к исследованию функции
p
(
X, Z
) =
μ
1
X
2
+
μ
3
Z
2
−
2
γZ
+ (2
−
μ
3
)
γ
2
на множестве
ν
1
X
2
+
ν
3
Z
2
≥
ν
3
γ
2
.
Диапазон значений функции зависит от знаков при квадратах пере-
менных.
Если
μ
3
= 0
(т.е.
ν
2
=
ν
3
), но
γ
6
= 0
(т.е.
q
6
=
−
1
/
2
), то функция
p
(
X, Z
)
линейна по
Z
и ее множество значений — вся числовая ось.
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2007. № 1
7