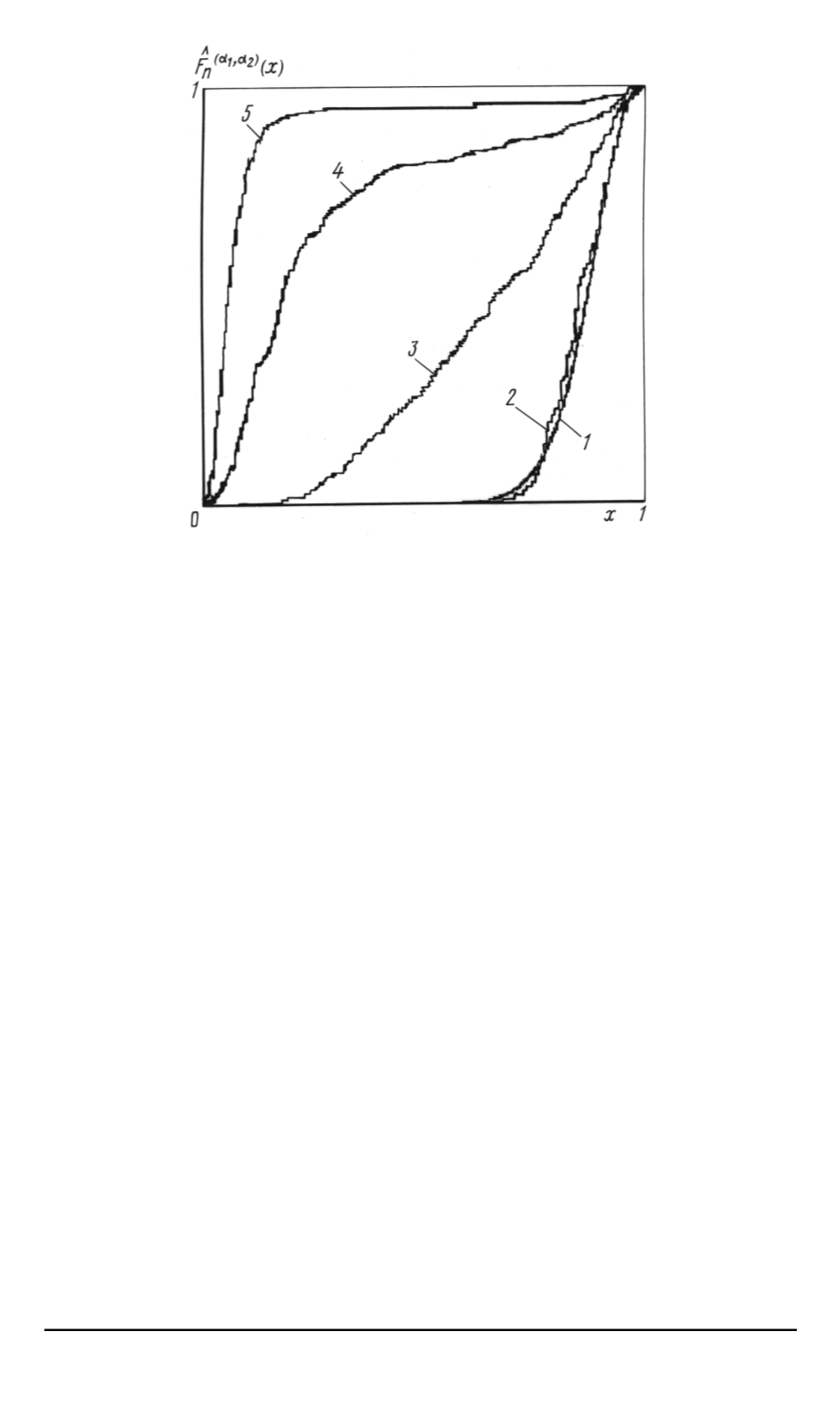
Рис
. 8.
Эмпирическая функция распределения
Разработанная программа моделирования
(
см
.
рис
. 7)
позволила
провести численные эксперименты при различных значениях параме
-
тров
μ
,
p
2
и начальных условиях
α
1
,
α
2
.
Полученные эмпирические
функции распределения при больших значениях
α
2
аналогичны пред
-
ставленным на рис
. 7
и позволяют сделать следующий вывод
.
Посколь
-
ку при стремлении параметра
p
2
к единице эмпирическая функция
распределения сходится к ступенчатой с единственным разрывом в
нуле
,
то в случае
p
2
= 1
имеет место нормировка для числа финаль
-
ных частиц
,
отличная от линейной
.
Таким образом
,
в рассматривае
-
мой стохастической эпидемической модели случай удаления
p
1
>
0
и случай неудаления
p
1
= 0
из популяции зараженных особей имеют
качественное различие
.
В первом случае число выживших здоровых
особей примерно пропорционально начальному их числу
,
а во втором
случае число выживших здоровых особей
—
меньше
.
Решение задачи о нахождении нормировки для
η
(
α
1
,α
2
)
в случае
p
2
= 1
и вывод предельной теоремы для числа финальных частиц
возможны аналитическими методами через построение решения урав
-
нения
(20) [18].
Брюсселятор
.
Стационарное распределение
.
Рассматривается
марковский процесс
ξ
(
t
) = (
ξ
1
(
t
)
, ξ
2
(
t
))
,
t
2
[0
,
∞
)
,
на множестве
состояний
N
2
,
соответствующий схеме взаимодействий
[6]
2
T
1
+
T
2
→
3
T
1
;
T
1
→
0
, T
2
; 0
→
T
1
.
(23)
68
ISSN 1812-3368.
Вестник МГТУ им
.
Н
.
Э
.
Баумана
.
Сер
. “
Естественные науки
”. 2005.
№
2


