уравнения для стационарных вероятностей
;
установлена асимптотиче
-
ская нормальность стационарного распределения
{
q
j
}
при большой ин
-
тенсивности
λ
0
поступления новых частиц
.
Теорема
3
[19].
Рассмотрим схему взаимодействий
2
T
→
T,
0
→
T
.
Обозначим
η
=
η
(
λ
0
)
целочисленную случайную величину с
распределеним
{
q
j
, j
= 0
,
1
,
2
, . . .
}
.
Положим
x
2
(
−∞
,
∞
)
.
Тогда
lim
λ
0
→∞
P
n
η
(
λ
0
)
−
c
1
λ
0
c
2
√
λ
0
≤
x
o
=
1
√
2
π
Z
x
−∞
e
−
y
2
/
2
dy,
где
c
1
>
0
,
c
2
>
0
—
некоторые константы
.
Для схемы взаимодействий
(11)
описанным выше методом стати
-
стического моделирования получены оценки вероятностей стационар
-
ного распределения
b
q
j
,
j
2
N
,
вычисленные как отношение суммарно
-
го времени нахождения процесса в состоянии
j
ко всему времени моде
-
лирования
T
:
b
q
j
=
m
X
l
=1
τ
l
j
/T
,
τ
l
j
—
время нахождения процесса в состо
-
янии
j
при
l
-
м попадании в это состояние
∞
X
j
=0
b
q
j
= 1
.
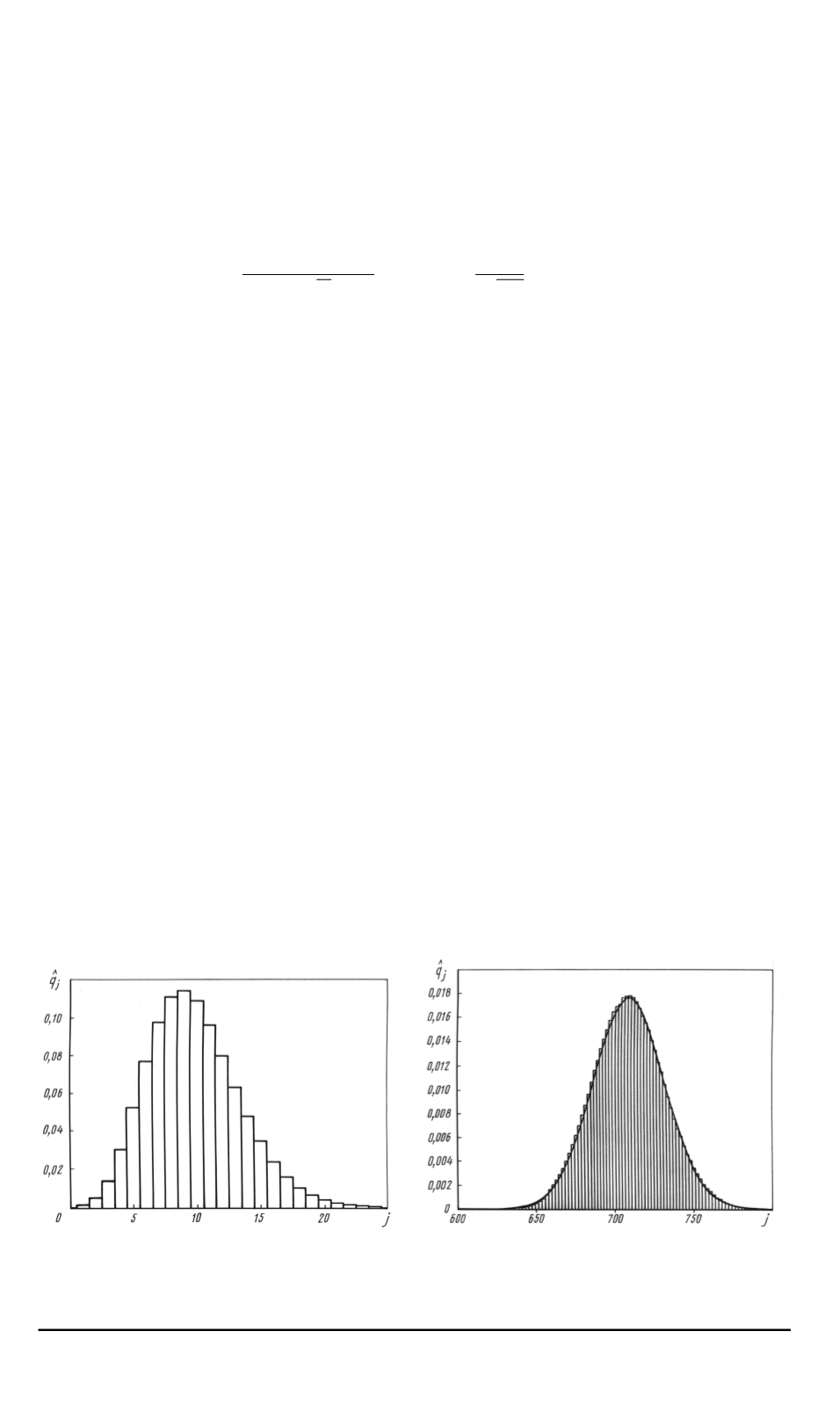
На рис
. 4
при
-
ведена гистограмма для
{
b
q
j
}
при следующих значениях параметров
:
λ
2
= 2
,
λ
1
= 15
,
λ
0
= 50
;
p
2
3
= 1
/
4
,
p
2
1
= 3
/
4
,
p
1
2
= 2
/
3
,
p
1
0
= 1
/
3
;
T
= 25348
.
На рис
. 5
дана гистограмма для
{
b
q
j
}
при значениях пара
-
метров
λ
2
= 2
,
λ
1
= 15
,
λ
0
= 500000
;
p
2
3
= 1
/
4
,
p
2
1
= 3
/
4
,
p
1
2
= 2
/
3
,
p
1
0
= 1
/
3
;
T
= 6
,
5953
.
Сравнивая гистограммы
,
приведенные на рис
. 4
и рис
. 5,
видим
,
что
при увеличении параметра
λ
0
они близки к нормальной плотности рас
-
пределения
;
выборочные средние и дисперсия
—
параметры кривой
нормального закона на рис
. 5 —
вычислены по стандартным форму
-
лам
.
Аналогичные численные результаты получены при других значе
-
Рис
. 4.
Гистограмма стационарного
распределения при
λ
0
= 50
Рис
. 5.
Гистограмма стационарного
распределения при
λ
0
= 500 000
ISSN 1812-3368.
Вестник МГТУ им
.
Н
.
Э
.
Баумана
.
Сер
. “
Естественные науки
”. 2005.
№
2
63


