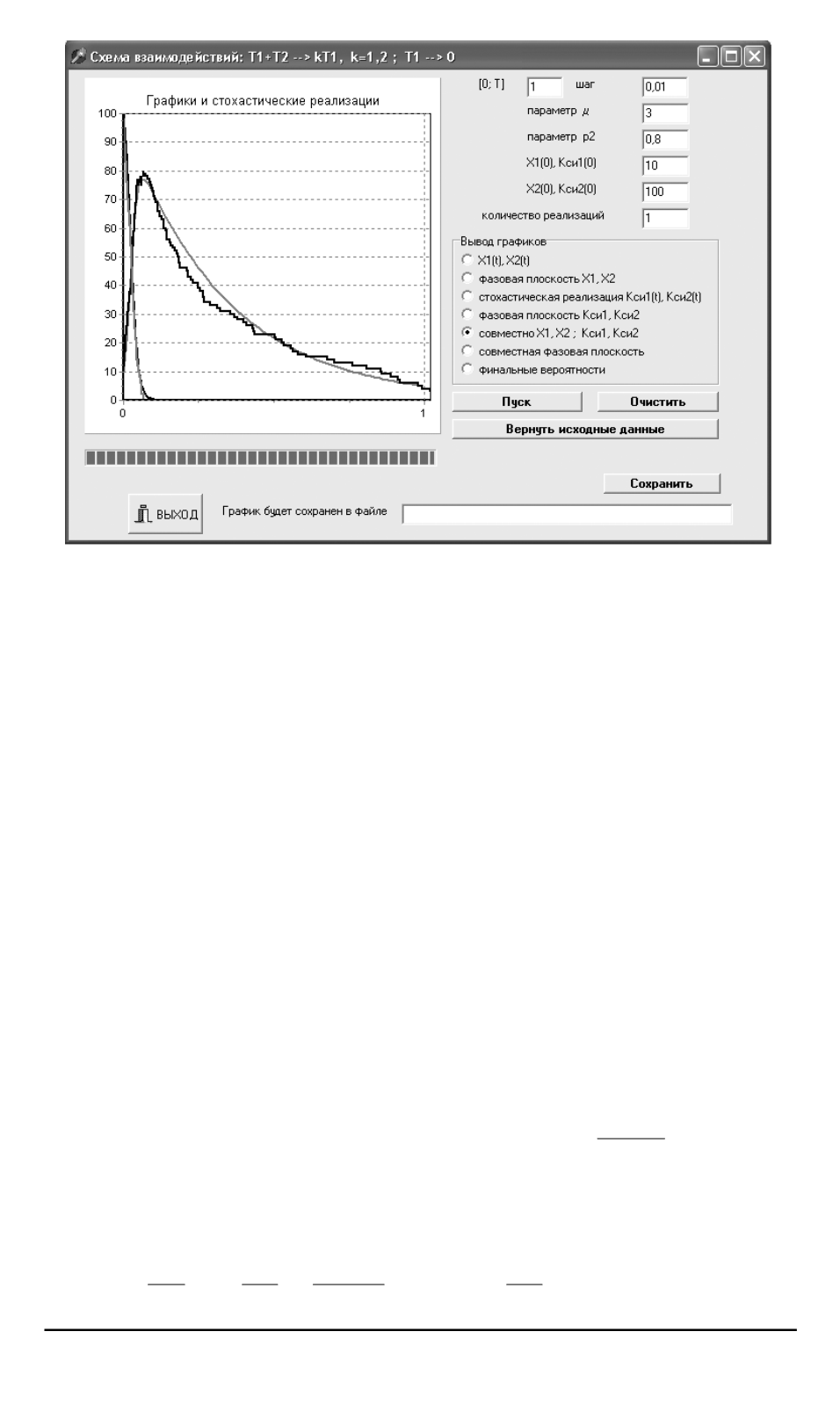
Рис
. 7.
Детерминированная модель
x
1
(
t
)
,
x
2
(
t
)
и стохастические реализации
ξ
1
(
t
)
,
ξ
2
(
t
)
где
x
1
(
t
)
—
количество больных особей
,
x
2
(
t
)
—
количество особей
,
восприимчивых к инфекционному заболеванию в детерминированной
модели эпидемии
.
Взаимосвязь вероятностного и детерминистическо
-
го описаний для различных схем эпидемий рассматривалась в
[12, 13]
и др
.
На рис
. 7
дана траектория детерминированной модели
x
1
(
t
)
,
x
2
(
t
)
при начальных условиях
x
1
(0) = 10
,
x
2
(0) = 100
,
и приведен при
-
мер реализации стохастического процесса эпидемии
(
ξ
1
(
t
)
, ξ
2
(
t
))
при
начальных условиях
(
ξ
1
(0)
, ξ
2
(0)) = (10
,
100)
.
Значения параметров
следующие
:
μ
= 3
,
p
2
= 0
,
8
,
T
= 1
.
С вероятностью
,
равной
1,
процесс
ξ
(
t
)
остановится в одном из по
-
глощающих состояний
(0
, γ
2
)
,
γ
2
= 0
,
1
,
2
, . . .
(
остались только здоро
-
вые особи
).
Для финальных вероятностей
q
(
α
1
,α
2
)
(0
,γ
2
)
= lim
t
→∞
P
(
α
1
,α
2
)
(0
,γ
2
)
(
t
)
вводим производящие функции
(
|
s
| ≤
1
)
f
(
α
1
,α
2
)
(
s
) =
∞
X
γ
2
=0
q
(
α
1
,α
2
)
(0
,γ
2
)
s
γ
2
, g
(
z
1
, z
2
;
s
) =
∞
X
α
1
,α
2
=0
z
α
1
1
z
α
2
2
α
1
!
α
2
!
f
(
α
1
,α
2
)
(
s
)
.
Стационарное первое уравнение Колмогорова получает вид
h
z
2
p
2
∂
2
∂z
2
1
+
p
1
∂
∂z
1
−
∂
2
∂z
1
∂z
2
+
μ
1
−
∂
∂z
1
i
g
(
z
1
, z
2
;
s
) = 0
(20)
66
ISSN 1812-3368.
Вестник МГТУ им
.
Н
.
Э
.
Баумана
.
Сер
. “
Естественные науки
”. 2005.
№
2


