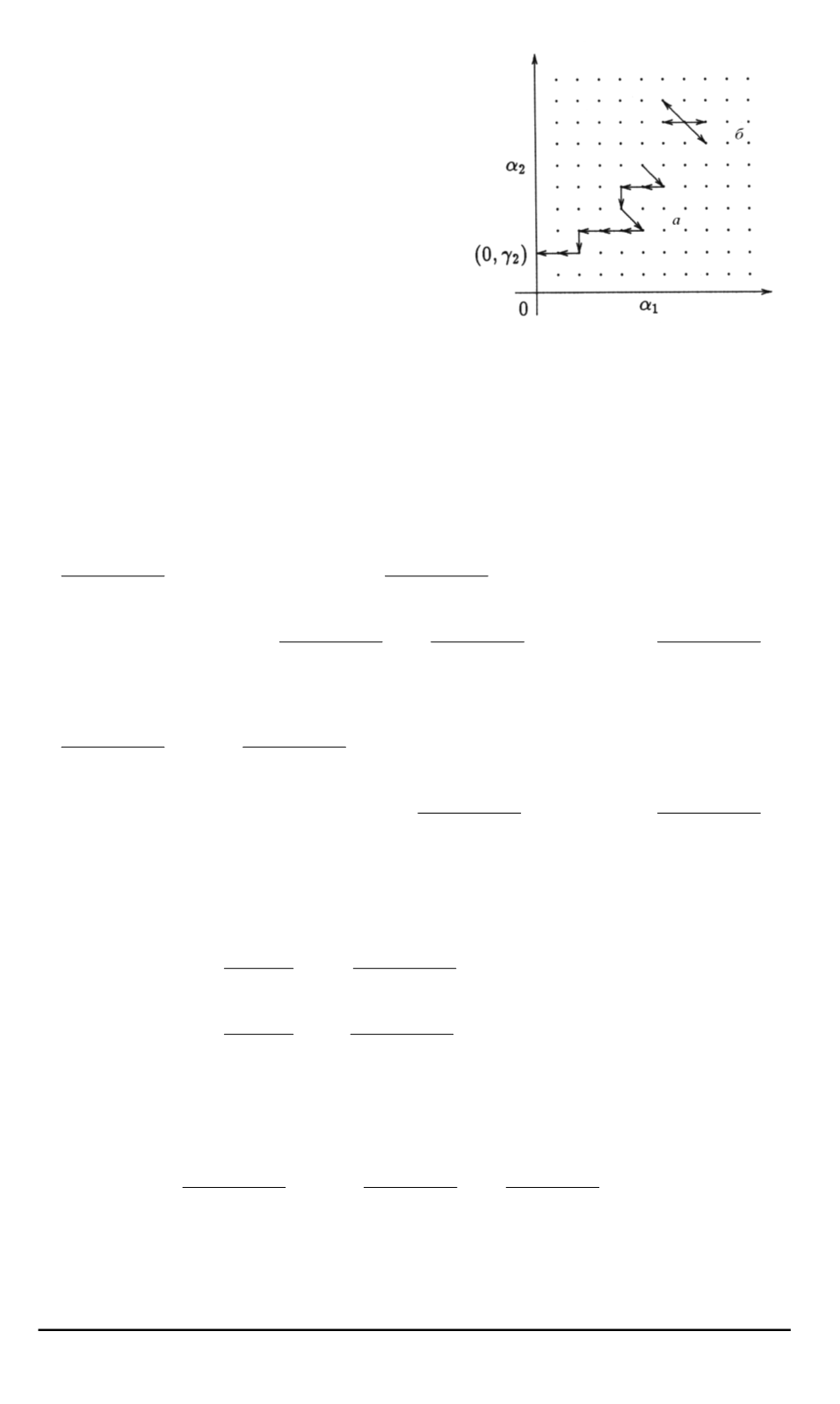
Рис
. 6.
Скачки марковских процес
-
сов на
N
2
соответствующее вектору
(
β
1
, β
2
−
1)
.
Кроме того
,
через случайное время
τ
1
(
β
1
,β
2
)
,
P
{
τ
1
(
β
1
,β
2
)
≤
t
}
= 1
−
e
−
μβ
1
t
,
больная особь умирает и процесс пе
-
реходит в состояние
,
соответствую
-
щее вектору
(
β
1
−
1
, β
2
)
.
Случай
-
ные величины
τ
1
(
β
1
,β
2
)
,
τ
2
(
β
1
,β
2
)
неза
-
висимы
;
в состоянии
(
β
1
, β
2
)
про
-
цесс находится случайное время
τ
(
β
1
,β
2
)
= min(
τ
1
(
β
1
,β
2
)
, τ
2
(
β
1
,β
2
)
)
.
Случай
p
1
= 1
называется
моделью эпидемии
Вейса
[13],
а случай
p
2
= 1
называется
моделью эпидемии Бартлетта
–
Мак
-
Кендрика
[14].
Чтобы получить детерминированное приближение для процесса
ξ
(
t
)
,
соответствующего схеме взаимодействий
(17),
дифференцируем
второе уравнение
(18)
по
s
1
и
s
2
;
получаем
∂
2
F
α
(
t
;
s
)
∂s
1
∂t
= 2
p
2
s
1
+
p
1
−
s
2
∂
2
F
α
(
t
;
s
)
∂s
1
∂s
2
+
+
p
2
s
2
1
+
p
1
s
1
−
s
1
s
2
∂
3
F
α
(
t
;
s
)
∂s
2
1
∂s
2
−
μ
∂F
α
(
t
;
s
)
∂s
1
+
μ
1
−
s
1
∂
2
F
α
(
t
;
s
)
∂s
2
1
,
∂
2
F
α
(
t
;
s
)
∂s
2
∂t
=
−
s
1
∂
2
F
α
(
t
;
s
)
∂s
1
∂s
2
+
+
p
2
s
2
1
+
p
1
s
1
−
s
1
s
2
∂
3
F
α
(
t
;
s
)
∂s
1
∂s
2
2
+
μ
1
−
s
1
∂
2
F
α
(
t
;
s
)
∂s
1
∂s
2
.
Подставив
s
= 1
и используя обозначения для среднего числа частиц
типа
T
i
,
A
i
(
t
) = (
∂F
α
(
t
;
s
)
/∂s
i
)
|
s
=1
,
i
= 1
,
2
,
получаем равенства
dA
1
(
t
)
dt
=
p
2
∂
2
F
α
(
t
;
s
)
∂s
1
∂s
2
s
=1
−
μA
1
(
t
)
,
dA
2
(
t
)
dt
=
−
∂
2
F
α
(
t
;
s
)
∂s
1
∂s
2
s
=1
.
(19)
Предположим
,
что при большом начальном числе частиц
α
=
= (
nα
1
, nα
2
)
,
n
→ ∞
,
выполнено условие
“
предельного перехода
” [1]
∂
2
F
α
(
t
;
s
)
∂s
1
∂s
2
s
=1
≈
∂F
α
(
t
;
s
)
∂s
1
s
=1
∂F
α
(
t
;
s
)
∂s
2
s
=1
;
тогда из
(19)
приходим к системе дифференциальных уравнений
˙
x
1
=
p
2
x
1
x
2
−
μx
1
,
˙
x
2
=
−
x
1
x
2
,
x
1
(0) =
x
0
1
, x
2
(0) =
x
0
2
,
ISSN 1812-3368.
Вестник МГТУ им
.
Н
.
Э
.
Баумана
.
Сер
. “
Естественные науки
”. 2005.
№
2
65


