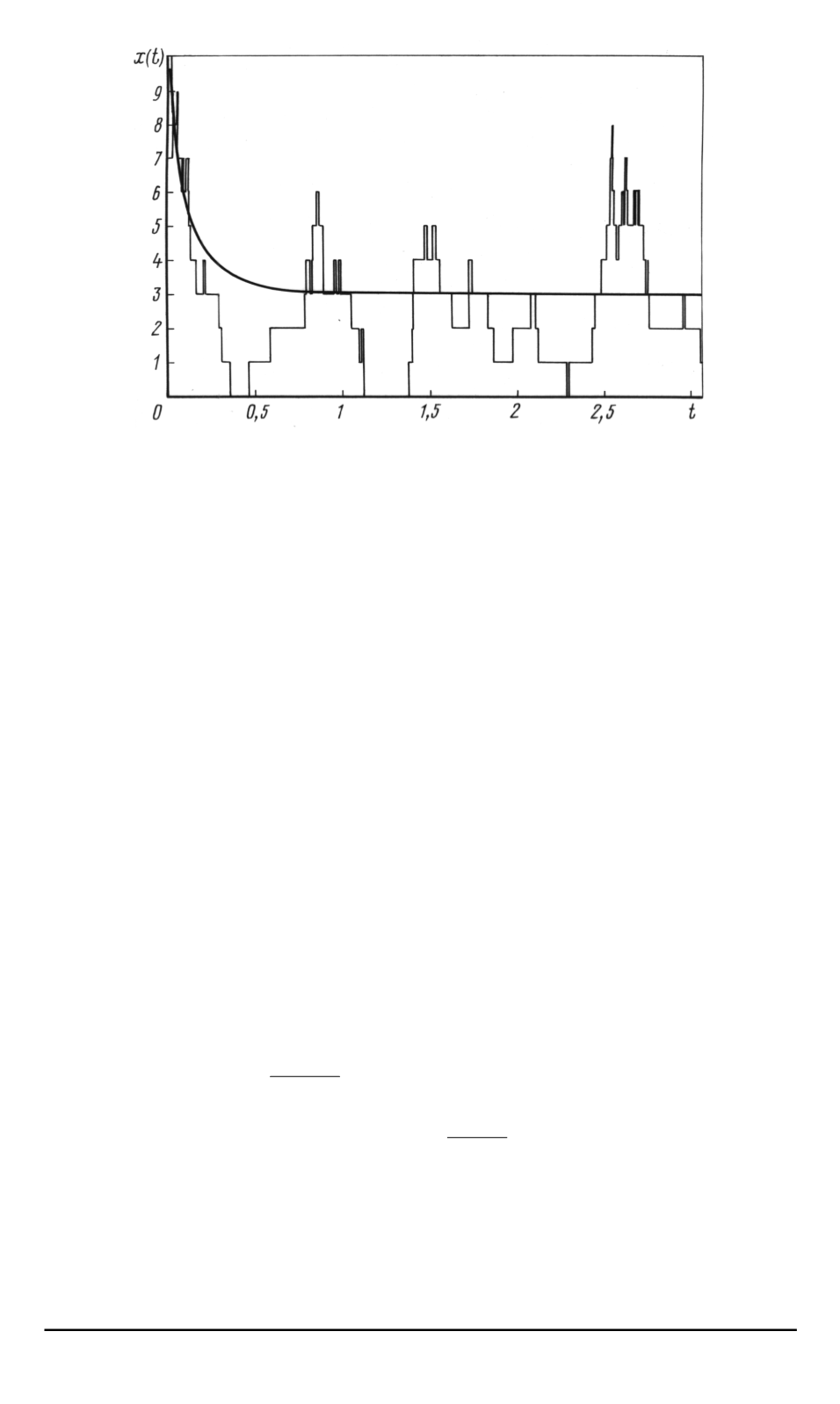
Рис
. 3.
Детерминированная модель
x
(
t
)
и стохастическая реализация
ξ
(
t
)
как уравнение популяционной динамики с внутривидовой конкурен
-
цией
[11].
На рис
. 3
дана траектория детерминированной модели
x
(
t
)
при на
-
чальном условии
x
(0) = 10
и приведен пример реализации стохасти
-
ческого процесса
ξ
(
t
)
при начальном условии
ξ
(0) = 10
.
Значения па
-
раметров составляют
:
λ
2
= 2
,
λ
1
= 4
,
5
,
λ
0
= 4
,
5
;
p
2
3
= 1
/
4
,
p
2
1
= 3
/
4
,
p
1
2
= 2
/
3
,
p
1
0
= 1
/
3
;
T
= 3
,
0688
.
Схема
(11)
интерпретируется как система попарно взаимодейству
-
ющих частиц с притоком частиц извне
[4, 5].
При
p
2
3
<
1
/
2
вследствие
формул
(13)
можно показать
[2,
гл
. 7, § 4],
что в системе при
t
→ ∞
су
-
ществует стационарное распределение
,
определяемое распределением
вероятностей
{
q
j
, j
= 0
,
1
,
2
, . . .
}
,
где
q
j
= lim
t
→∞
P
ij
(
t
)
.
Выражения
для стационарных вероятностей
q
j
известны
[2],
но малопригодны для
асимптотического исследования
.
Уравнение для производящей функ
-
ции стационарных вероятностей
f
(
s
) =
∞
X
j
=0
q
j
s
j
,
|
s
| ≤
1
,
имеет вид
λ
2
(
p
2
3
s
3
+
p
2
1
s
−
s
2
)
∂
2
f
(
s
)
∂s
2
+
+
λ
1
(
p
1
2
s
2
+
p
1
0
−
s
)
∂f
(
s
)
∂s
+
λ
0
(
s
−
1)
f
(
s
) = 0
.
(16)
Уравнение
(16)
сводится к гипергеометрическому уравнению
,
одна
-
ко исследовать свойства стационарного распределения
,
рассматривая
функцию
f
(
s
)
,
не удается
[19].
Уравнение
(16)
при
λ
1
= 0
и
p
2
1
= 1
является частным случаем рассмотренного в работе
[19]
более общего
62
ISSN 1812-3368.
Вестник МГТУ им
.
Н
.
Э
.
Баумана
.
Сер
. “
Естественные науки
”. 2005.
№
2


