где
λ
i
>
0
,
i
= 1
, . . . , n
, —
коэффициенты пропорциональности
.
Для
марковского процесса
ξ
(
t
)
по определению полагаем
a
αα
=
−
l
X
i
=1
ϕ
i
α
, a
αβ
=
l
X
i
=1
ϕ
i
α
p
i
β
−
α
+
ε
i
, α
6
=
β, α, β
2
N
n
.
Процесс
ξ
(
t
)
интерпретируется как стохастическая модель системы
взаимодействующих частиц
n
типов
T
1
, . . . , T
n
.
Событие
{
ξ
(
t
) =
β
}
есть такое состояние системы
,
в котором в момент времени
t
имеется
совокупность
S
β
частиц
,
состоящая из
β
1
частиц типа
T
1
,
. . . , β
n
частиц
типа
T
n
:
S
β
=
β
1
T
1
+
. . .
+
β
n
T
n
.
Зададим
l
комплексов взаимодействия
частиц
S
ε
i
,
соответствующих векторам
ε
i
.
Через случайное время
τ
i
β
,
P
{
τ
i
β
≤
t
}
= 1
−
e
−
ϕ
i
β
t
,
происходит взаимодействие комплекса частиц
S
ε
i
.
В этот момент из
β
1
частиц типа
T
1
выбирается
ε
i
1
частиц
,
. . . ,
из
β
n
частиц типа
T
n
выбирается
ε
i
n
частиц и этот комплекс частиц
S
ε
i
с
распределением вероятностей
{
p
i
γ
}
заменяется совокупностью
S
γ
но
-
вых частиц
.
Система из состояния
S
β
,
соответствующего вектору
β
,
переходит в состояние
S
β
−
ε
i
+
γ
,
соответствующее вектору
β
−
ε
i
+
γ
(
см
.
рис
. 1),
и далее происходит аналогичная эволюция системы частиц
.
В состоянии
S
β
система находится случайное время
τ
β
,
пока не про
-
изойдет какое
-
либо одно из
l
взаимодействий
,
т
.
е
.
τ
β
= min(
τ
1
β
, . . . , τ
l
β
)
.
Предполагается
,
что случайные величины
τ
1
β
, . . . , τ
l
β
независимы
.
Тогда
P
{
τ
β
≤
t
}
= 1
−
e
−
(
ϕ
1
β
+
...
+
ϕ
l
β
)
t
и вероятность события
,
что произошло
взаимодействие комплекса частиц
S
ε
i
при условии
,
что взаимодействие
произошло
,
равна
ϕ
j
β
(
P
l
i
=1
ϕ
i
β
)
−
1
.
Возможные превращения частиц в
такой системе представляются схемой взаимодействий
(1),
где случай
-
ный вектор
γ
i
= (
γ
i
1
, . . . , γ
i
n
)
имеет распределение
{
p
i
γ
}
,
i
= 1
, . . . , l
.
Выбор значений
(8)
для
ϕ
i
β
объясняется следующим образом
.
Пусть
марковский процесс находится в состоянии
β
= (
β
1
, . . . , β
n
)
,
что со
-
ответствует наличию совокупности частиц
S
β
=
β
1
T
1
+
. . .
+
β
n
T
n
.
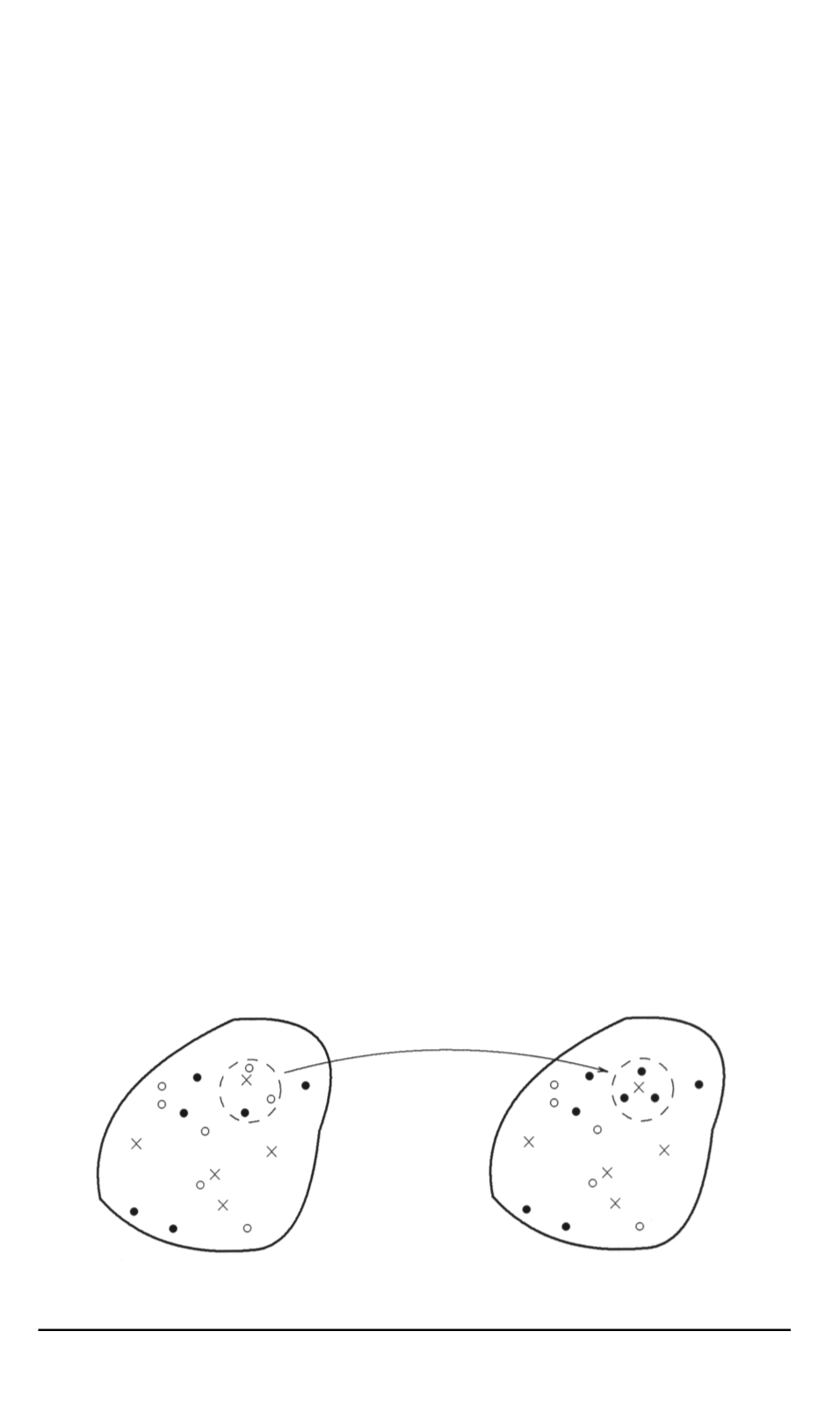
Рис
. 1.
Взаимодействие комплекса частиц
T
1
+ 2
T
2
+
T
3
→
T
1
+ 3
T
3
ISSN 1812-3368.
Вестник МГТУ им
.
Н
.
Э
.
Баумана
.
Сер
. “
Естественные науки
”. 2005.
№
2
57


