Рис
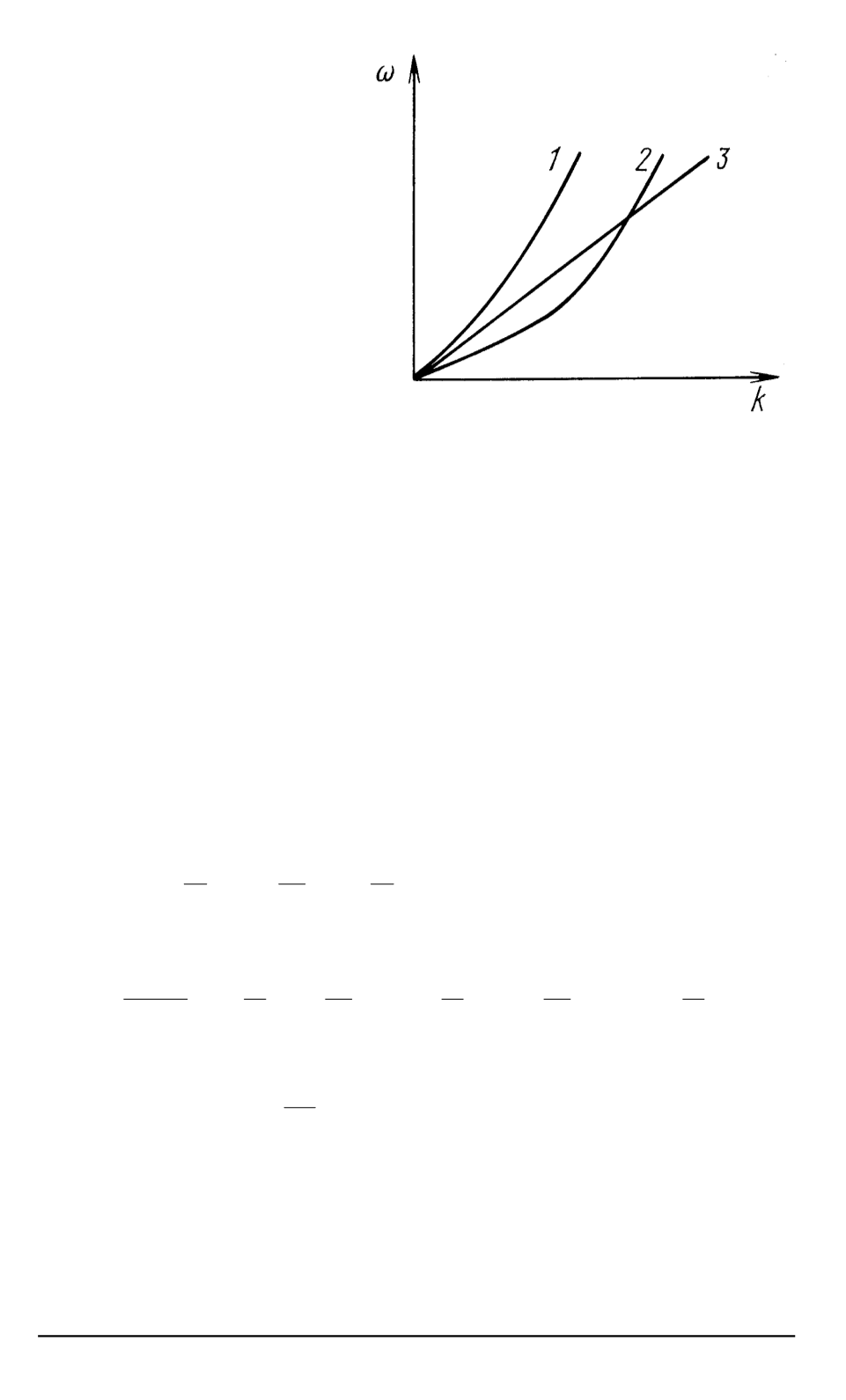
. 1.
Взаимное расположение ветвей
дисперсионного соотношения
ω
=
ω
(
k
)
:
1
—
быстрая ветвь
,
2
—
медленная ветвь
,
3
—
ω
=
kV
двух точек пересечения с
обеими ветвями
.
В случае
V
2
=
ν
−
−
ν
−
ν
,
где
ν >
0
,
прямая
ω
=
kV
не пере
-
секает ветвей при
k >
0
;
следовательно
,
решением
системы будет простая уе
-
диненная волна
.
В случае
V
2
=
ν
+
−
ν
+
ν
,
ν >
0
,
пря
-
мая
ω
=
kV
при
k >
0
пе
-
ресекает медленную ветвь
;
следовательно
,
имеет ме
-
сто резонанс длинной мед
-
ленной и короткой быстрой
волн
.
Бегущие волны описы
-
ваются динамической систе
-
мой
,
эквивалентной уравнениям
(4):
˙
u
1
=
u
3
,
˙
u
2
=
u
4
,
˙
u
3
=
α
1
(
ν
±
)
u
1
−
βu
2
+
F
1
,
˙
u
4
=
α
2
(
ν
±
)
u
2
−
βu
1
+
F
2
,
(7)
где
β
= 2
κm
−
1
u
01
u
02
;
α
i
(
V
2
)
,
i
= 1
,
2
,
—
функции
,
зависящие от ско
-
рости распространения волн
:
α
i
(
V
2
) =
ρ
0
m
µ
µ
i
−
3
κ
ρ
0
u
2
0
i
−
κ
ρ
0
u
2
0
j
−
V
2
¶
,
i, j
= 1
,
2
,
i
6
=
j
;
нелинейные функции
F
i
,
i
= 1
,
2
,
имеют вид
F
i
=
νν
±
ρ
0
m
u
i
−
κ
m
u
3
i
−
3
κ
m
u
0
i
u
2
i
−
κ
m
u
i
u
2
j
−
2
κ
m
u
0
j
u
i
u
j
−
κ
m
u
0
i
u
2
j
.
Представим систему
(7)
в матричном виде
:
dw
dξ
=
A
(
ν
±
)
w
+
F
(
ν, w
)
,
где
w
= (
u
1
, u
2
, u
3
, u
4
)
т
,
(0
,
0
, F
1
, F
2
)
т
,
A
¡
V
2
¢
=
0
0 1 0
0
0 0 1
α
1
(
V
2
)
−
β
0 0
−
β α
2
(
V
2
) 0 0
.
ISSN 1812-3368.
Вестник МГТУ им
.
Н
.
Э
.
Баумана
.
Сер
. “
Естественные науки
”. 2004.
№
3
61


