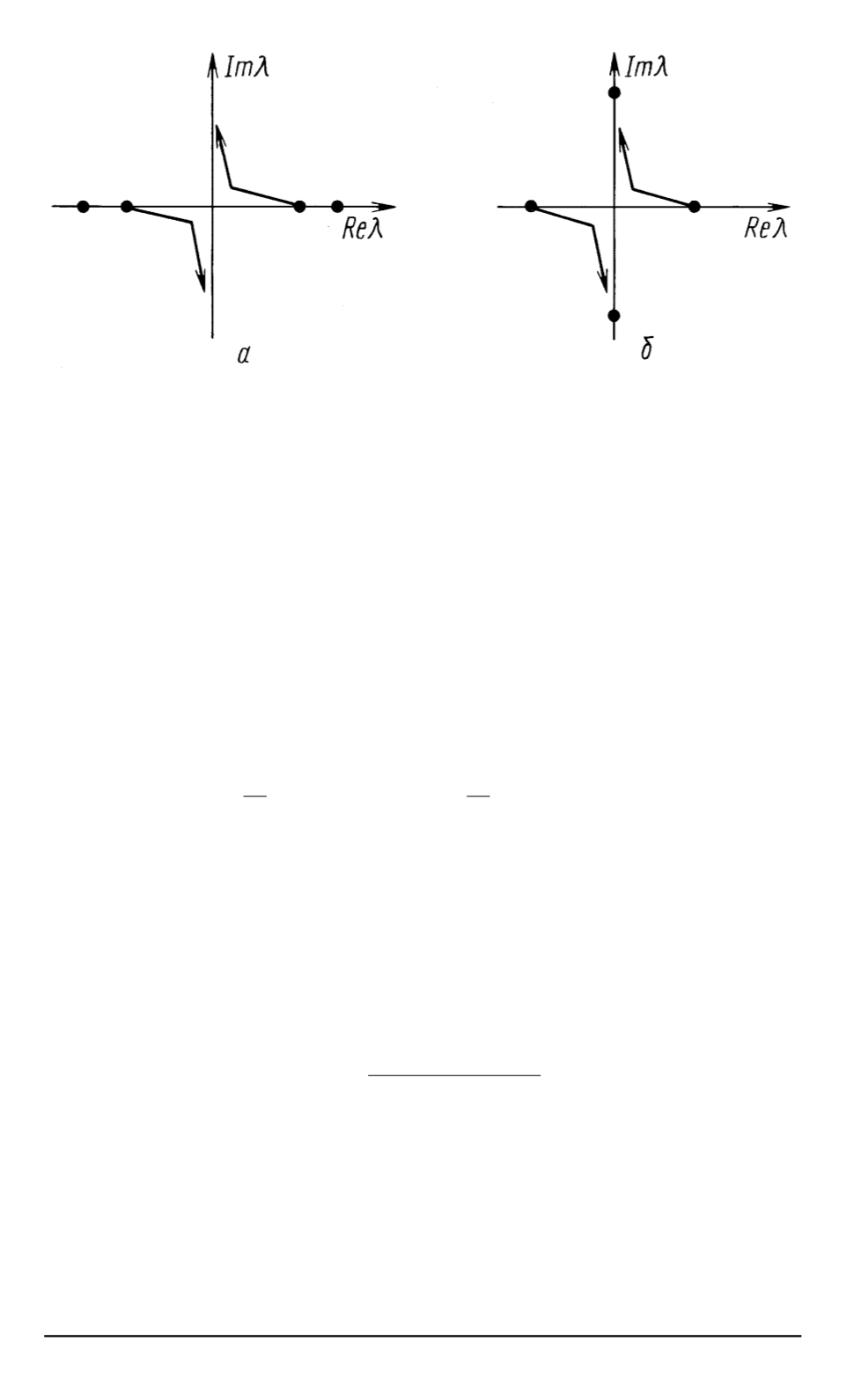
Рис
. 2.
Изменение собственных значений матрицы
A
(
V
2
)
в комплексной плос
-
кости спектрального параметра
λ
при прохождении
ν
через нуль
:
а
—
для
V
2
=
ν
−
−
ν
−
ν
,
б
—
для
V
2
=
ν
+
−
ν
+
ν
Характеристическое уравнение
|
A
(
V
2
)
−
λI
|
= 0
имеет следующий
вид
:
λ
4
−
λ
2
¡
α
1
¡
V
2
¢
+
α
2
¡
V
2
¢¢
+
α
1
¡
V
2
¢
α
2
¡
V
2
¢
−
β
2
= 0
.
(8)
Это же уравнение можно получить из дисперсионного соотношения
заменой
λ
=
ik
,
V
=
ω/k
.
Из соотношения
(5)
следует
,
что характери
-
стическое уравнение
(8)
принимает вид
³
λ
2
−
ρ
0
m
¡
ν
+
−
V
2
¢ ´³
λ
2
−
ρ
0
m
¡
ν
−
−
V
2
¢ ´
= 0
.
(9)
Расположение собственных значений в комплексной плоскости спек
-
трального параметра
λ
при прохождении
ν
через нуль изображено на
рис
. 2.
При
V
2
=
ν
±
на мнимой оси лежат следующие корни характери
-
стического уравнения
(9):
при
V
2
=
ν
−
—
нуль второго порядка
;
при
V
2
=
ν
+
—
нуль второго порядка и два ненулевых значения
λ
=
±
iq
,
где
q
=
p
ρ
0
m
−
1
(
ν
+
−
ν
−
)
.
Солитонные решения
.
При
V
2
=
ν
−
−
ν
имеем простую бифур
-
кацию
,
для которой на рис
. 2,
а
представлено изменение собственных
значений матрицы
A
(
V
2
)
(
корней уравнения
(9)),
перемещающихся с
действительной оси на мнимую при прохождении
ν
через нуль
.
Поло
-
жим
w
=
w
0
+
w
1
,
где
w
0
∈
E
0
,
w
1
∈
E
1
,
E
0
и
E
1
—
соответственно
62
ISSN 1812-3368.
Вестник МГТУ им
.
Н
.
Э
.
Баумана
.
Сер
. “
Естественные науки
”. 2004.
№
3


