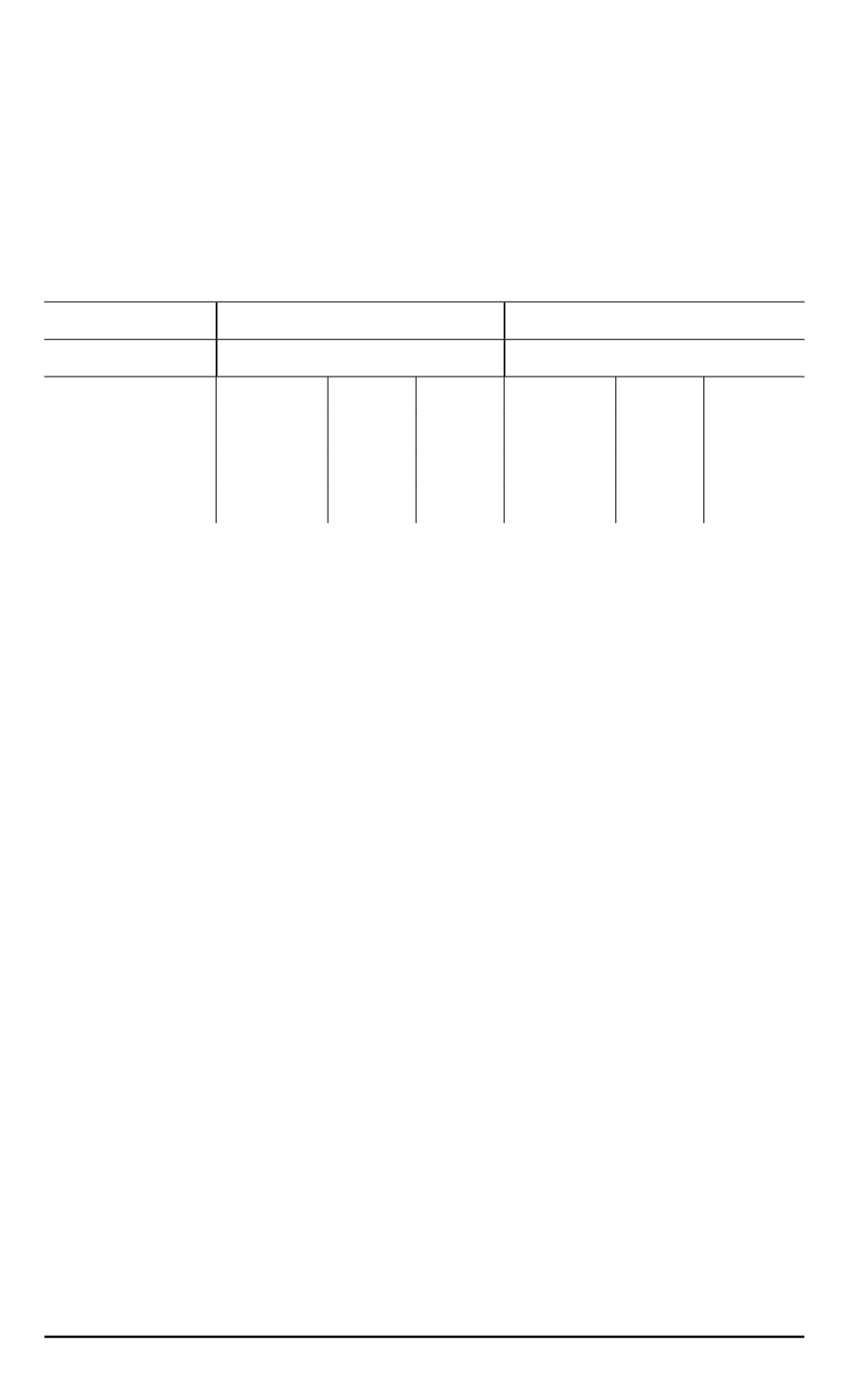
В таблице приведены двусторонние оценки поперечников
d
n
(
W
,
H
)
,
n
=
1
,
2
,
3,
полученные при условии
δ
≤
10
−
4
и
δ
≤
5
·
10
−
5
на сет
-
ках с количеством узлов
N
=
25
и
N
=
40
соответственно
.
Для условия
δ
≤
5
·
10
−
5
в приложении
2
также приведены графики весовой функ
-
ции
p
и первых собственных функций оператора
T
σ
,
соответствующие
оптимальной мере
σ
.
Оценки поперечников
d
n
(
W
,
H
)
Отн
.
погрешность
δ
=
10
−
4
δ
=
5
·
10
−
5
N
25
40
n
1
2
3
1
2
3
Оценка снизу
0,276217 0,209453 0,175184 0,276217 0,209453 0,175184
Точное значение
0,276217. . .
— — 0,276217. . .
— —
Оценка сверху
0,276221 0,209474 0,175201 0,276219 0,209456 0,175192
Отметим
,
что удается достичь весьма незначительного расхожде
-
ния верхней и нижней оценок величин
d
n
(
W
,
H
)
,
n
≥
2.
Это позволяет
рассчитывать на возможность совмещения интегральных оценок попе
-
речников
d
n
(
W
,
H
)
при
n
≥
2
в классе мер
(7).
Приложение
1.
Сформулируем и докажем лемму о свойствах соб
-
ственных значений
λ
и собственных функций
f
следующей краевой
задачи
:
f
00
(
x
)+
λ
p
(
x
)
f
(
x
) =
0
,
x
∈
[
a
,
b
]
,
(25)
f
0
(
a
) =
−
λ
m
0
f
(
a
)
,
(26)
f
0
(
b
) =
λ
m
1
f
(
b
)
,
(27)
где
m
0
,
m
1
—
положительные числа
,
p
—
положительная непрерывная
(
или кусочно непрерывная
)
на отрезке
[
a
,
b
]
функция
.
Лемма
.
Задача
(
25
)
–
(
27
)
имеет бесконечно много неотрицатель
-
ных собственных значений
λ
0
,
λ
1
,
λ
2
, . . .
,
образующих монотонно воз
-
растающую последовательность
,
где
λ
n
→
∞
при
n
→
∞
.
Кроме того
,
собственная функция
,
соответствующая
λ
n
,
имеет ровно
n
нулей в ин
-
тервале
(
a
,
b
)
.
Доказательство леммы
,
приводимое далее
,
в значительной мере
повторяет представленное в работе
[7]
доказательство аналогичного
утверждения для случая стандартных краевых условий
:
f
(
a
)
cos
α
−
f
0
(
a
)
sin
α
=
0
,
84 ISSN 0236-3933.
Вестник МГТУ им
.
Н
.
Э
.
Баумана
.
Сер
. "
Естественные науки
". 2003.
№
2


