
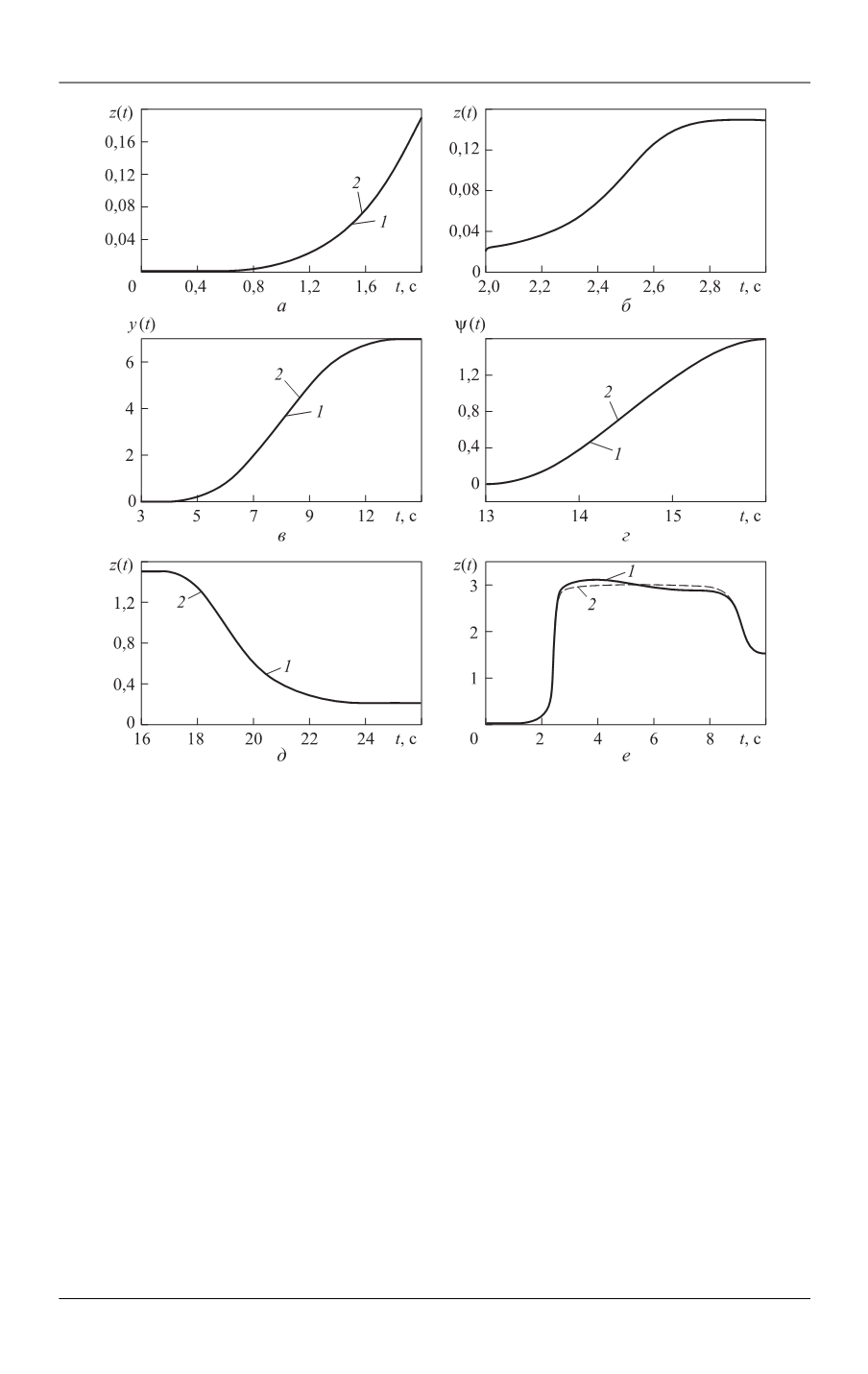
Решение задачи терминального управления для плоской системы…
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. Естественные науки. 2016. № 6
131
Изменение координат
( )
z t
на этапах 1 (
а
) и 2 (
б
),
( )
y t
на этапе 3 (
в
),
( )
t
на этапе 4 (
г
),
( )
z t
на этапе 5 (
д
),
( )
z t
на этапе 2 выполнения маневра при
2
=10 с
T
(
е
)
выхода. На этапе 3 управления по переменной
y
наблюдается хорошее следова-
ние по заданной траектории (часть
в
рисунка). При этом координата
x
остается
равной нулю, а координата
z
— координате .
d
z
За промежуток времени
3
4
T T
переменная
изменяется от заданного
начального положения до заданного конечного (часть
г
рисунка).
На этапе 5 координата
z
плавно уменьшается до заданного конечного зна-
чения, точно следуя заданной программной траектории (часть
д
рисунка).
В конце этого этапа квадрокоптер останавливается, чтобы переключить управ-
ление, и выполняет посадку.
Отметим, что указанный подход требует тонкой настройки параметров: ес-
ли время выполнения маневра на этапе 2 задать слишком большим, то про-
граммная траектория приближается к границам коридора, а отклонение от про-
граммной траектории может достигать достаточно больших значений (часть
е
рисунка).
















