находится с помощью метода перевала
[13, 14].
Функция
S
(
u
)
является
однозначной аналитической функцией в области
Re
u >
0
с разрезом
по отрезку
[0
,
1]
и имеет простую точку перевала
u
0
,
определяемую из
условия
S
0
(
u
0
) = 0
.
Дифференцируя функцию
S
(
u
)
,
находим
u
0
=
1
2
+
1
2
r
1 +
2
a
b
,
S
00
(
u
0
) =
4
b
2
a
r
1 +
2
a
b
,
S
000
(
u
0
) =
−
8
b
2
a
µ
3 +
2
b
a
¶
,
S
(4)
(
u
0
) =
96
b
4
a
3
µ
1 +
a
b
¶r
1 +
2
a
b
.
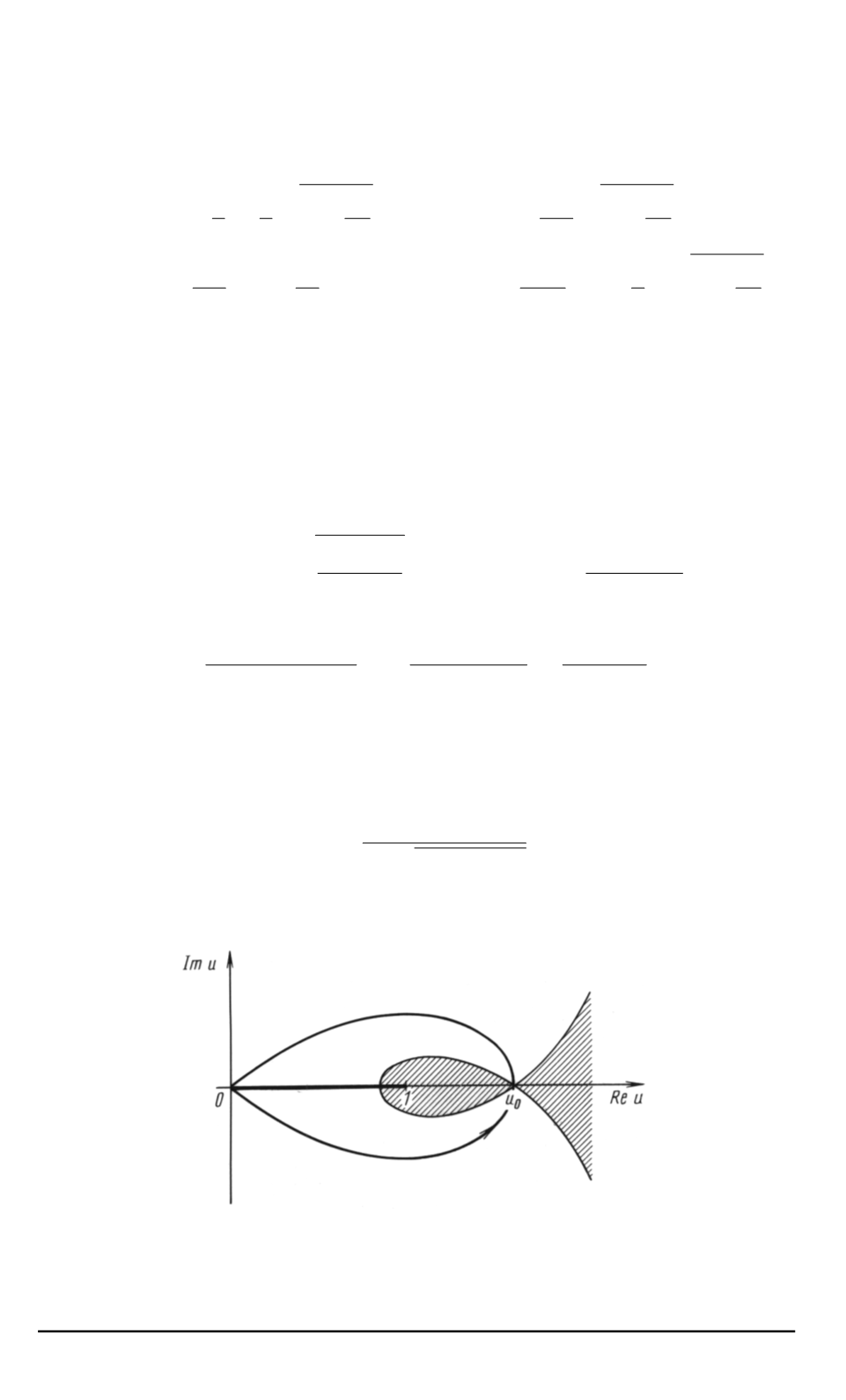
Контур интегрирования может быть деформирован в петлю
,
про
-
ходящую через точку
u
0
и лежащую при
u
6
=
u
0
в области
Re
S
(
u
)
<
<
Re
S
(
u
0
)
(
рис
. 5).
В рассматриваемом случае выполнены условия те
-
оремы
7.1
из работы
[14,
гл
. 4].
Согласно этой теореме асимптотика ин
-
теграла
(35)
с точностью до второго члена определяется выражением
(1+)
Z
0
e
νS
(
u
)
h
(
u
)
du
∼
ω
s
2
π
νS
00
(
u
0
)
e
νS
(
u
0
)
Ã
h
(
u
0
)
−
1
4
νS
00
(
u
0
)
×
×
µ
2
h
00
(
u
0
)
−
2
S
000
(
u
0
)
h
0
(
u
0
)
S
00
(
u
0
)
+
µ
5(
S
000
(
u
0
))
2
6(
S
00
(
u
0
))
2
−
S
(4)
(
u
0
)
2
S
00
(
u
0
)
¶
h
(
u
0
)
¶ !
.
(36)
Введем обозначение
R
ν
=
e
νS
(
u
0
)
aν
p
2
πνS
00
(
u
0
)
.
Рис
. 5.
Контур интегрирования в области
Re
S
(
u
)
<
Re
S
(
u
0
)
(
область
Re
S
(
u
)
>
Re
S
(
u
0
)
заштрихована
)
ISSN 1812-3368.
Вестник МГТУ им
.
Н
.
Э
.
Баумана
.
Сер
. “
Естественные науки
”. 2005.
№
1
17


