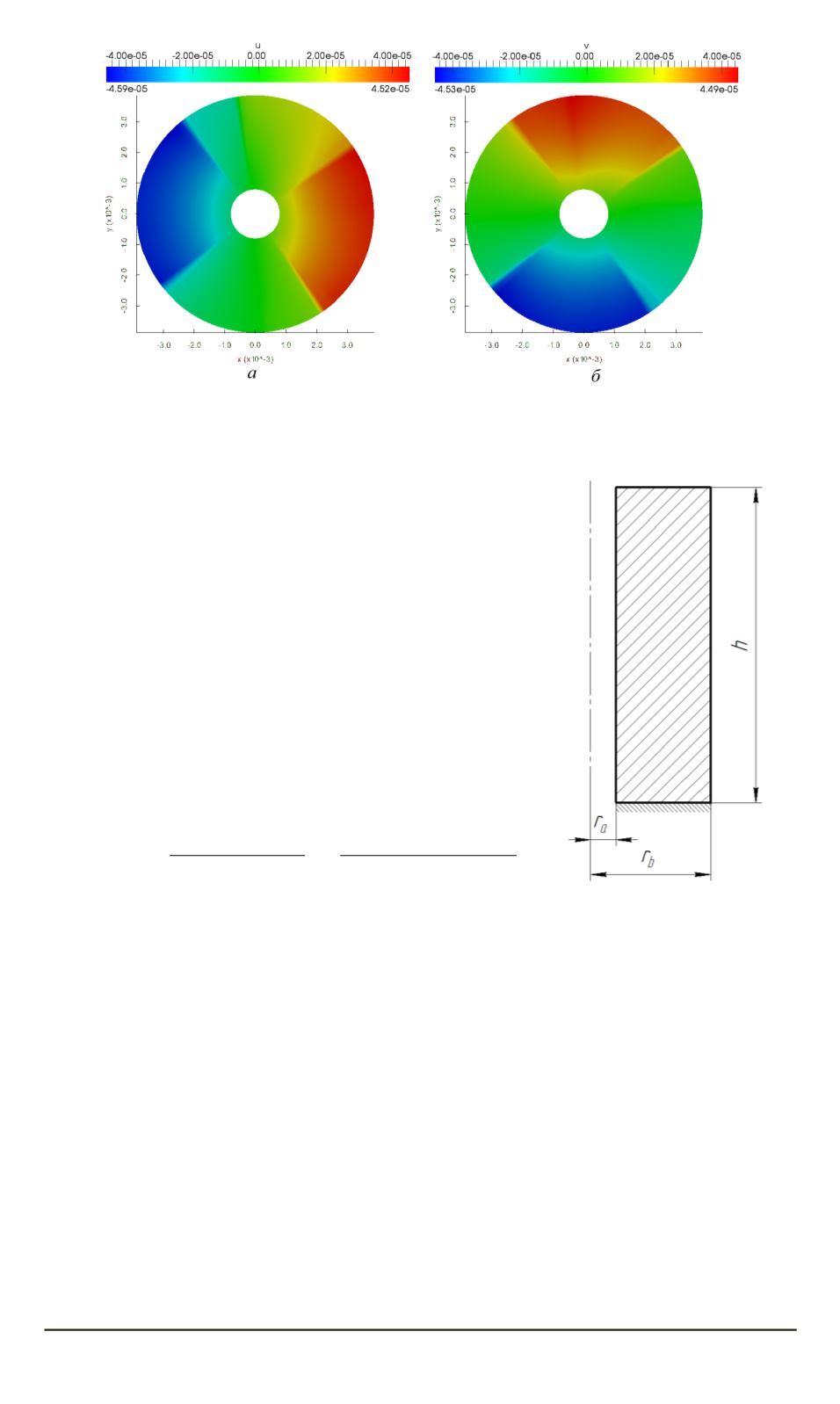
Рис. 6. Перемещения
u
(
а
) и
v
(
б
) на момент окончания расчета в горизонталь-
ном сечении таблетки
Рис. 7. Расчетная область
квазиодномерной задаче,
обозначим
~u
= (
u, w
)
т
. Граничные условия для этой
задачи в координатах
(
r, z
)
имеют следую-
щий вид:
w
|
z
=0
= 0;
σ
|
r
=
r
a
=
σ
|
r
=
r
b
=
σ
|
z
=
h
= 0
.
Примем, что температура распределена
по пространству линейно на каждом вре-
менн´ом слое. Выберем
T
1
(
t
)
и
T
2
(
t
)
в со-
ответствии с (8), тогда поле температуры
зададим так:
T
(
r, z, t
) =
T
1
(
t
)
−
T
2
(
t
)
r
a
−
r
b
r
+
T
2
(
t
)
r
a
−
T
1
(
t
)
r
b
r
a
−
r
b
.
Рассмотрим задачу с размерами обла-
сти, соответствующими размерам топлив-
ной таблетки
r
a
= 0
,
8
,
r
b
= 3
,
8
.
Распределения функций памяти
e
1
, e
2
, e
3
в различные моменты вре-
мени на сетке из 20 000 точек приведены на рис. 8, 9. Отметим, что при
более ранних моментах времени функция
e
1
равна единице, и лишь
впоследствии, когда трещина сформировалась, появляются растрес-
кавшиеся области. Это связано с отсутствием областей растяжения
в первом главном направлении тензора деформаций до тех пор, по-
ка трещина не сформировалась полностью в данной области. В зоне
ослабленного материала в одном направлении в модели размазанных
трещин поле напряжений теряет гладкость, поэтому в указанном на-
правлении возможны появление растягивающих напряжений и выпол-
нение критерия образования трещины.
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2014. № 6
109


