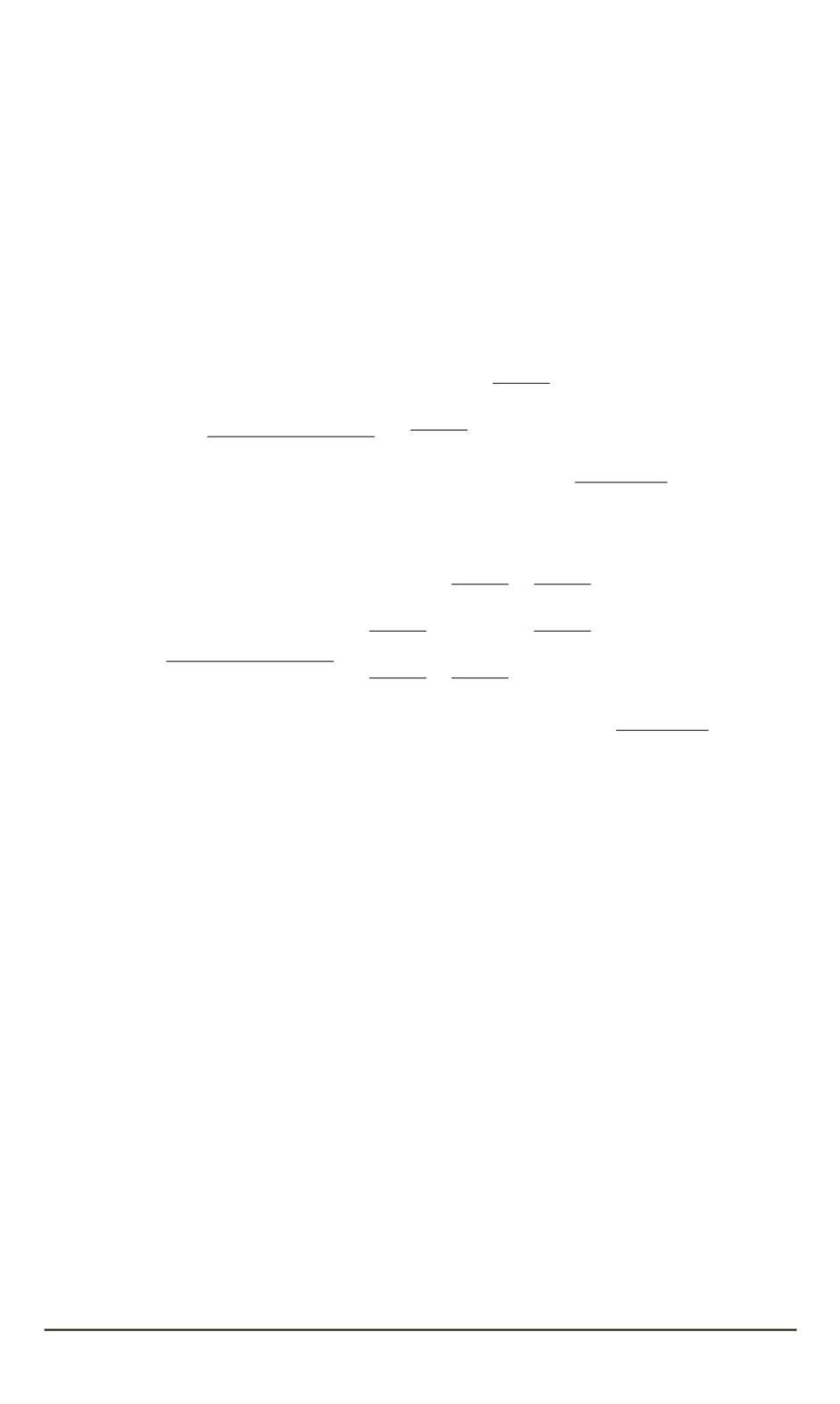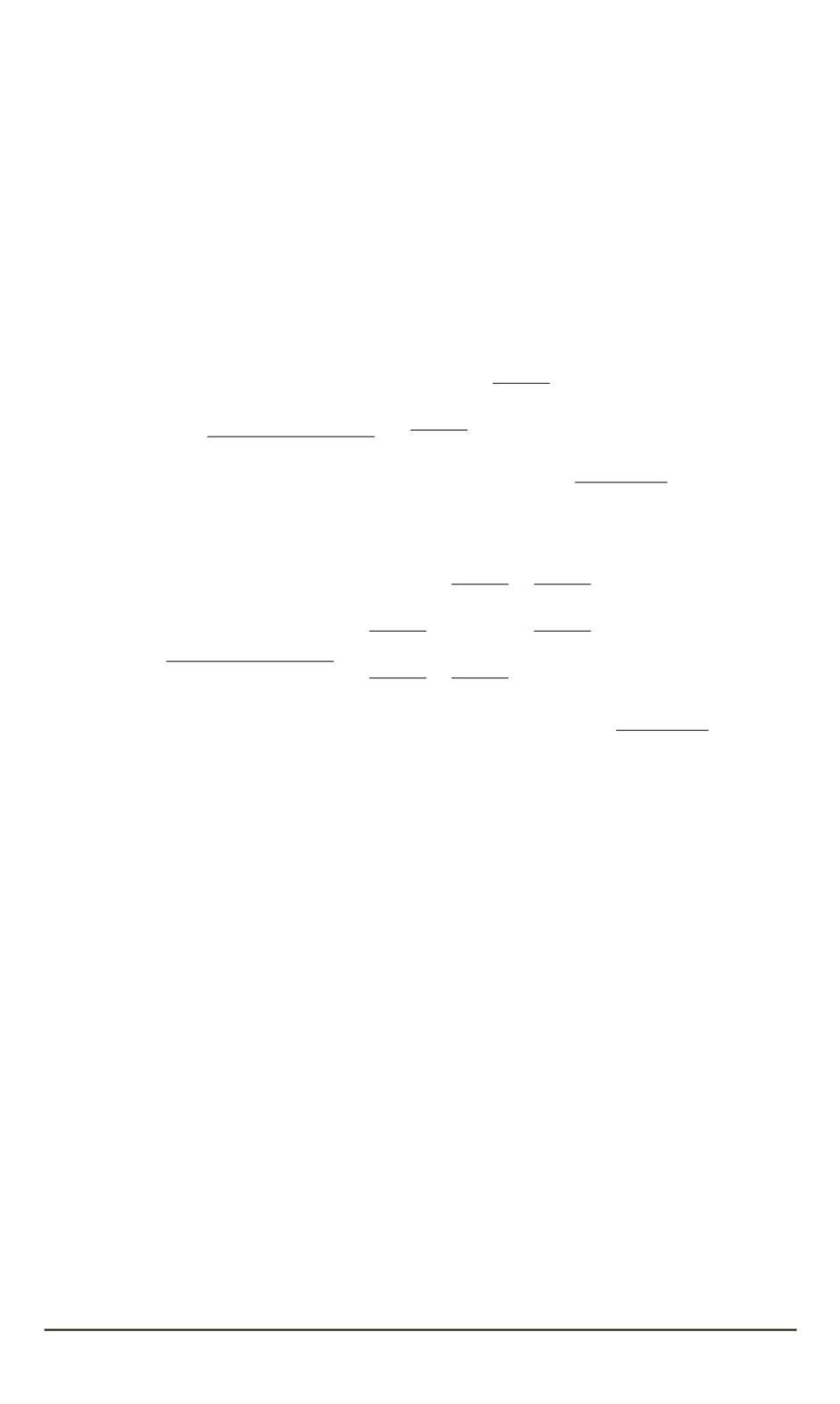
перемещений в виде
u
=
N
X
i
=1
4
X
j
=1
u
ij
e
ϕ
ij
(
x, y
)
, где
u
ij
— перемещения в
узлах, можно записать уравнения равновесия в слабой постановке и
перейти к системе линейных алгебраических уравнений [13, 14]:
[
K
(
e
1
, e
2
, e
3
)]
{
U
}
=
{
R
U
(
e
1
, e
2
, e
3
, T
)
}
.
Отметим, что вид матрицы жесткости
K
зависит от типа решаемой
двумерной задачи и используемой матрицы упругих коэффициентов.
В случае плоского деформированного состояния матрица упругих ко-
эффициентов имеет вид
C
=
E
1
−
ν
(1 +
ν
) (1
−
2
ν
)
1
ν
1
−
ν
0
ν
1
−
ν
1
0
0
0
1
−
2
ν
2 (1
−
ν
)
,
при решении осесимметричной задачи —
C
=
E
1
−
ν
(1 +
ν
) (1
−
2
ν
)
1
ν
1
−
ν
ν
1
−
ν
0
ν
1
−
ν
1
ν
1
−
ν
0
ν
1
−
ν
ν
1
−
ν
1
0
0
0
0
1
−
2
ν
2 (1
−
ν
)
.
Будем рассматривать изменение перемещений, деформаций и напря-
жений во времени, разбив временн´ой отрезок
[0
, t
f
]
на
P
временн ´ых
слоев с шагом
τ
=
t
f
/
(
P
−
1)
, на каждом из которых решается ста-
ционарная задача теории упругости с учетом температуры и влияния
размазанных трещин.
Для анализа рассмотренной математической модели разработан
программный комплекс, результаты тестирования которого приведе-
ны в работе [15].
Результаты расчетов.
Применим построенную модель разма-
занных трещин к моделированию разрушения топливной таблетки.
Диоксид урана обладает следующими физическими характеристика-
ми [18]: плотность
ρ
= 10 800
кг/м
3
; модуль Юнга
E
= 1
,
75
∙
10
11
Па;
коэффициент Пуассона
ν
'
0
,
316
; теплопроводность
λ
=3
,
487
Вт/(м
∙
K);
удельная теплоемкость
c
ε
= 310
Дж/(кг
∙
K); предел прочности
σ
f
=
= 1
,
1
∙
10
8
Па; коэффициент теплового расширения
α
= 10
−
5
K
−
1
.
Температуру естественного состояния примем равной
T
0
= 300
K.
Для полного описания трещин в таблетке недостаточно двумерной
постановки, поэтому рассмотрим два сечения:
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2014. № 6
105