Обобщенная трехмерная теория устойчивости упругих тел. Ч. 1. Конечные деформации - page 6

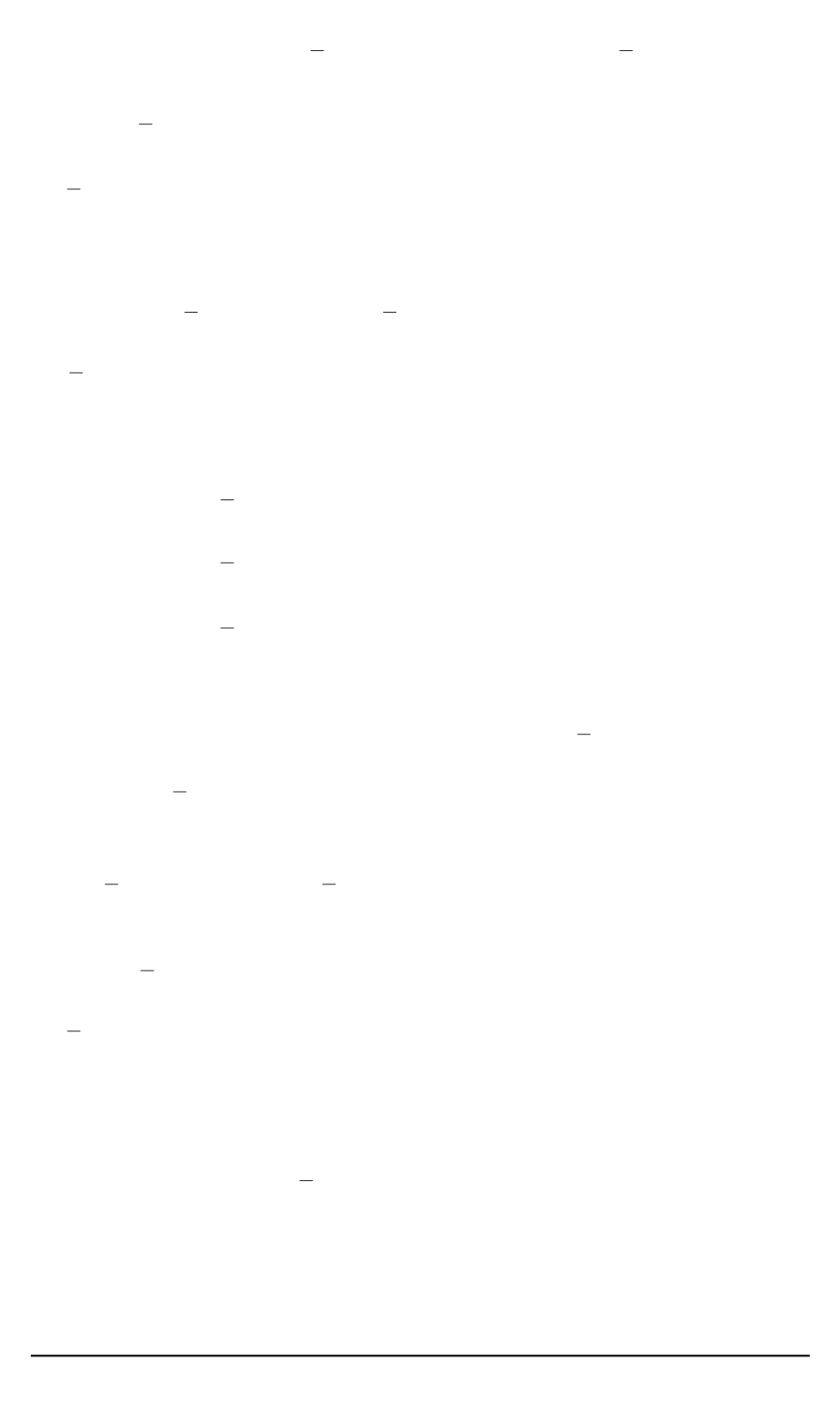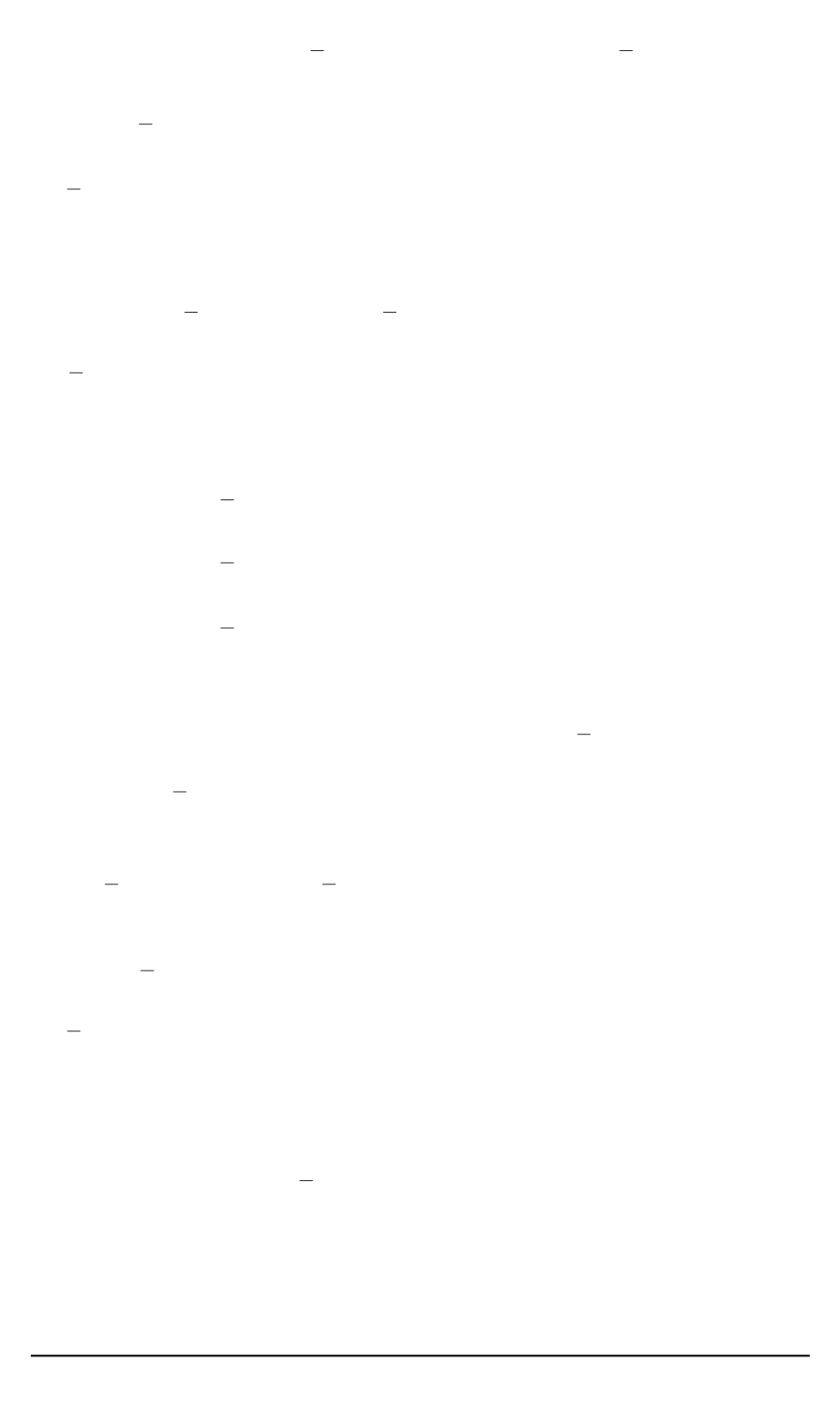
соотношениям C =
V
C =
1
2
(Fт · F − E) и Λ ≡
I
C = −
1
2
(F−1 · F– т − E) :
Λξ = −
1
2
(F−1
ξ · F – 1т + F−1 · F– 1т
ξ ) =
=
1
2
(F−1 ·∇⊗wт ·F – 1т +F −1 ·∇⊗ w· F – 1т ) = F−1 · ε (w)· F – 1т =
0
˜ε (w);
(20)
Cξ =
V
Cξ =
1
2
(Fт · F − E) ξ =
1
2
(Fт
ξ · F + Fт · F ξ) =
=
1
2
(Fт · ∇ ⊗ w · F + Fт · ∇ ⊗ wт · F) = Fт · ε (w) · F =
0
ε (w), (21)
где ε (w), 0ε(w),
0
˜ε (w) — тензоры линейной деформации,
ε (w) =
1
2
(∇ ⊗ w + ∇ ⊗ wт);
0
ε (w) =
1
2
(
0
∇ ⊗ w · F + Fт ·
0
∇ ⊗ wт);
0
˜ε (w) =
1
2
(U−2 ·
0
∇ ⊗ w · F – 1т + F −1 ·
0
∇ ⊗ wт · U−2 ).
(22)
Конвективные производные левых тензоров деформации Коши–
Грина и Альманзи, вычисляемых по J =
V
A =
1
2
(F · Fт + F · Fт) и
A ≡
I
A = − 1
2
(F — 1т · F−1 + F−1 т · F −1 ), находим аналогично конвек-
тивным производным правых тензоров деформаций (20) и (21) [16]:
Jξ =
1
2
(Fξ · F т+F · Fт
ξ ) =
1
2
(∇⊗wт· F · Fт +F ·F т·∇⊗w) = ˜ε (w), (23)
Aξ = −
1
2
(F−1т
ξ · F−1 + F−1т · F−1
ξ ) =
=
1
2
(∇ ⊗ w · F −1 т · F −1 + F−1 т · F −1 · ∇ ⊗ wт) = V −2 · ˜ε (w) · V −2 .
(24)
В (23) и (24) введен еще один тензор линейной деформации:
˜ε(w) =
1
2
(∇ ⊗ wт · V 2 + V2 · ∇ ⊗ w) , (25)
где V 2 — левый тензор искажений, V2 = F−1т · F −1 . Согласно приня-
той в работе [9] классификации, тензоры Λ и C являются первым и
пятым энергетическими тензорами деформации
(n)
C, n = I, V, а тензоры
84 ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2013. № 4