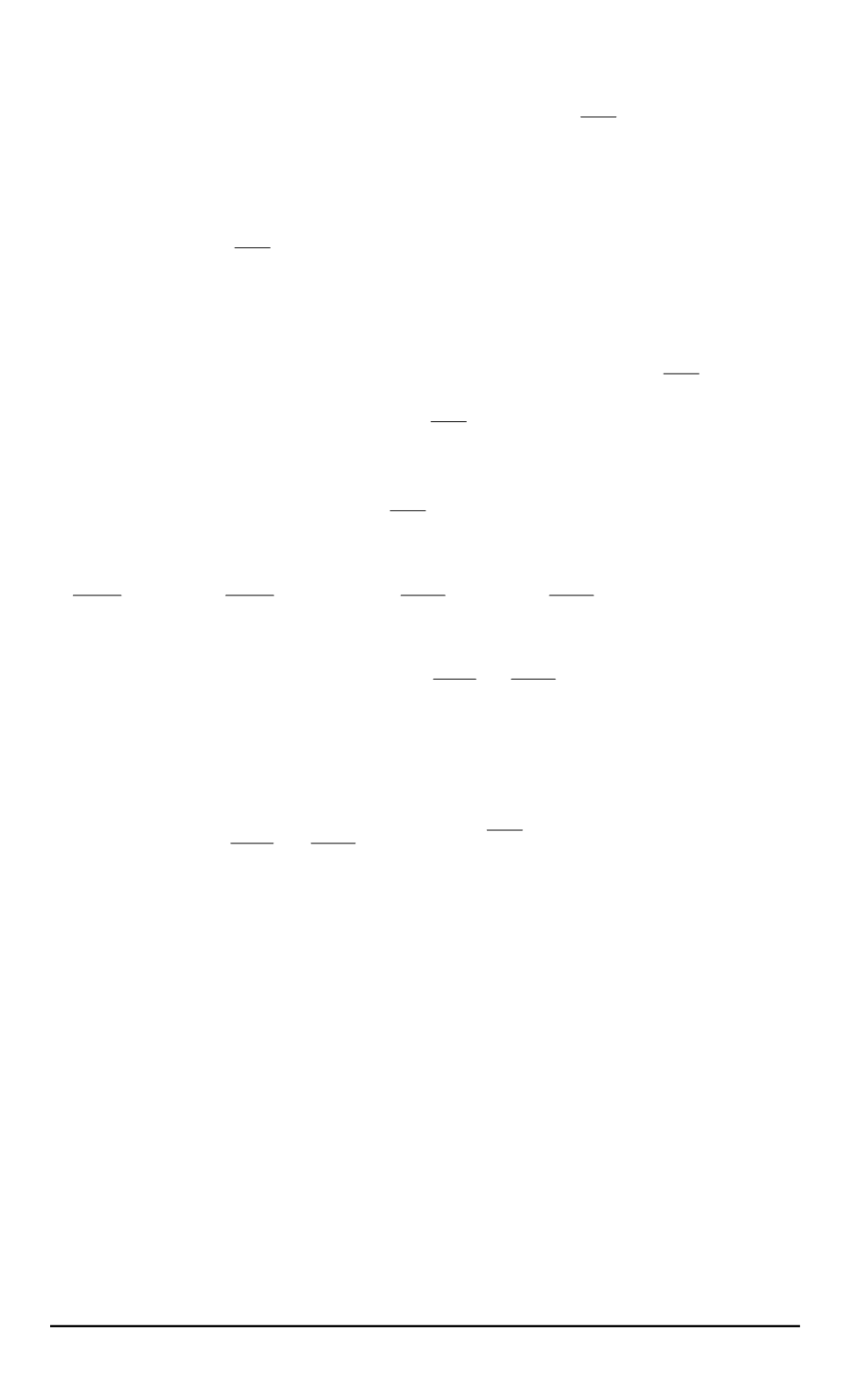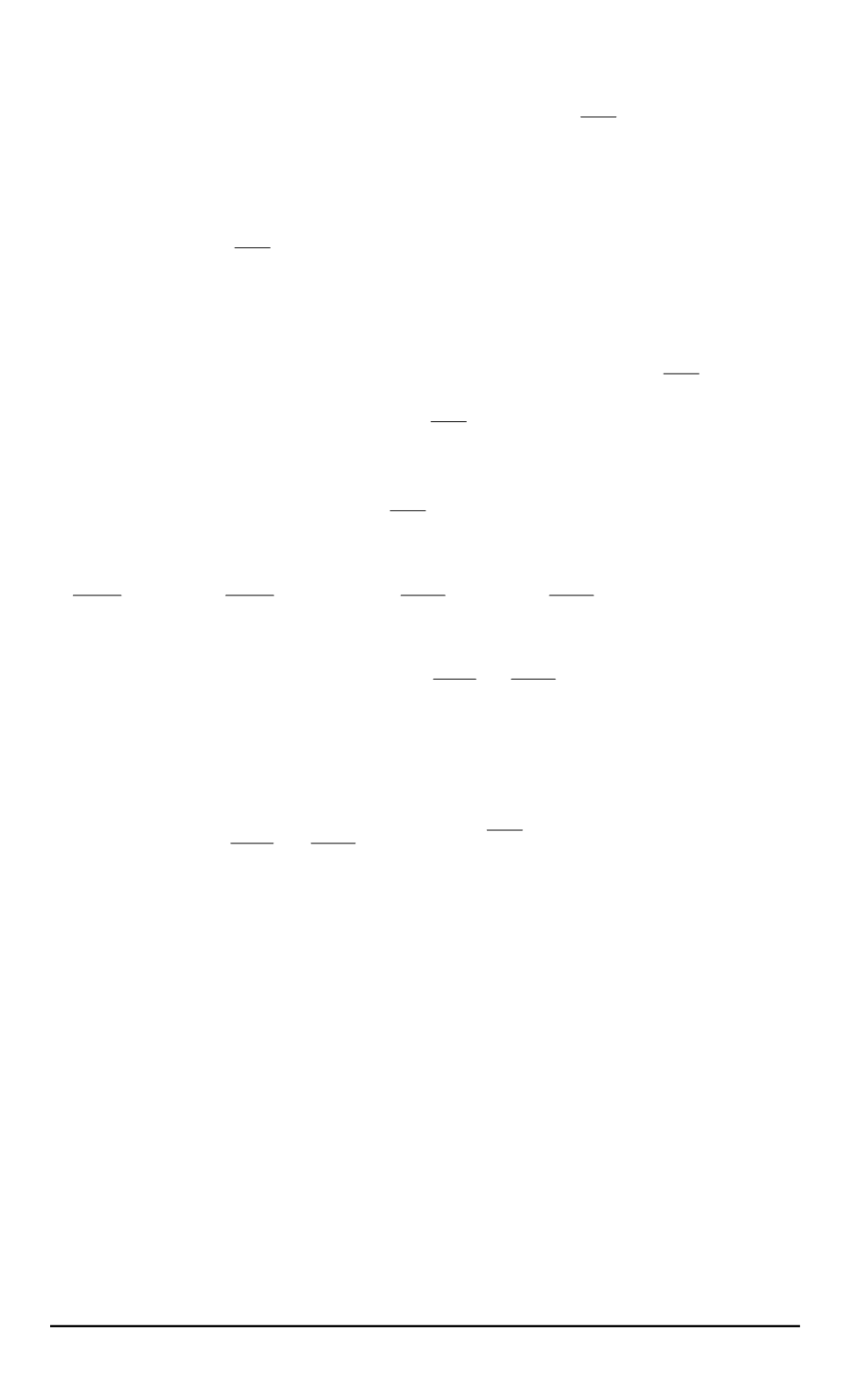
увеличением на единицу значения
α
1
. Мультииндекс с измененной
первой компонентой обозначим через
α
0
:
α
0
1
=
α
1
+ 1
,
α
0
k
=
α
k
, k
= 2
, p.
Рекуррентное соотношение, аналогичное соотношению (32), получим
в соответствии с (17), последовательно группируя в одно слагаемое
все члены ряда, имеющие первым левым сомножителем волну
X
k
по
каждому
x
k
,
k
= 1
, p
:
~P
α
0
=
p
X
k
=1
X
k
~U
k
, ~U
1
=
W
(
X
α
1
1
, . . . , X
α
p
p
)
~γ
α
0
,
~U
k
=
W
(
X
α
1
+1
1
, . . . , X
α
k
−
1
k
. . . X
α
p
p
)
~γ
α
0
, k
= 2
, p.
(37)
При этом для функций
~U
k
,
k
= 1
, p
, связанных по построению с
мультииндексом длины
m
, утверждение индукции выполнено.
Рассмотрим систему (9) при
~B
=
~P
α
0
. Воспользовавшись после
вычисления
A
k
∙
∂ ~P
α
0
/∂x
k
,
k
= 1
, p
, свойствами (20) и (21), получим
∂ ~P
α
0
∂t
−
s
−
1
X
k
=1
A
k
∂ ~P
α
0
∂x
k
=
p
X
k
=1
X
k
"
∂ ~U
k
∂t
−
p
X
k
=1
A
k
∂ ~U
k
∂x
k
#
+
+
t
p
X
k,j
=1
(
A
k
A
j
−
A
j
A
k
)
"
∂ ~U
j
∂x
k
−
∂ ~U
k
∂x
j
#
, p
≤
(
s
−
1)
.
(38)
Применив правило дифференцирования (23) к функциям
~U
k
, заданным
формулой (37), получим
∂ ~U
j
∂x
k
=
∂ ~U
k
∂x
j
,
k, j
= 1
, p, k
6
=
j.
Из (38) следует утверждение: если функции
~U
k
являются решением
системы (9), то и функция
~P
α
0
является решением системы (9). Утвер-
ждение индукции доказано для произвольного
(
s
−
1)
,
s >
3
.
Таким образом, для произвольного
s
,
s >
3
, рассмотрены все воз-
можные мультииндексы
α
, по которым выполняется суммирование
в ряде (8), и соответствующие им члены ряда, каждый из которых
является решением системы (27). В силу линейности системы и ана-
литичности рассматриваемых функций ряд (8) и любая его частичная
сумма, которая представляет собой нелинейную комбинацию бегущих
волн, также являются решением системы (27).
Замечание.
Выведем для двумерного мультииндекса правило диф-
ференцирования
W
-скобки волнового взаимодейстия (23), которое бы-
ло использовано в ходе доказательства теоремы. Применим метод ма-
тематической индукции с параметром индукции, равным порядку вол-
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2009. № 4
15