Итак, леваяи праваячасти уравнения(16) в точке
s
= 0
одновре-
менно становятся равными 1.
Далее, исследуем поведение левой и правой частей уравнения(16)
при малых по модулю отрицательных значениях
s
. Учитываяанали-
тичность левой и правой частей уравнения(16), вычислим их произ-
водные по
s
в точке
s
= 0
. Имеем
lim
s
→
0
∂
∂s
e
−
sG
0
=
−
G
0
,
lim
s
→
0
∂
∂s
Y
min
0
e
−
sy
dF
Y
(
y
) = lim
s
→
0
−
Y
min
0
e
−
sy
ydF
Y
(
y
) =
=
−
Y
min
0
ydF
Y
(
y
) =
−
m
Y
,
(18a)
где
m
Y
— математическое ожидание случайной величины
Y
. Посколь-
ку страховаяплата
G
0
складываетсяиз средних страховых выплат
m
Y
и рисковой надбавки, то всегда имеет место соотношение
G
0
> m
Y
,
(19)
или
−
G
0
<
−
m
Y
.
(20)
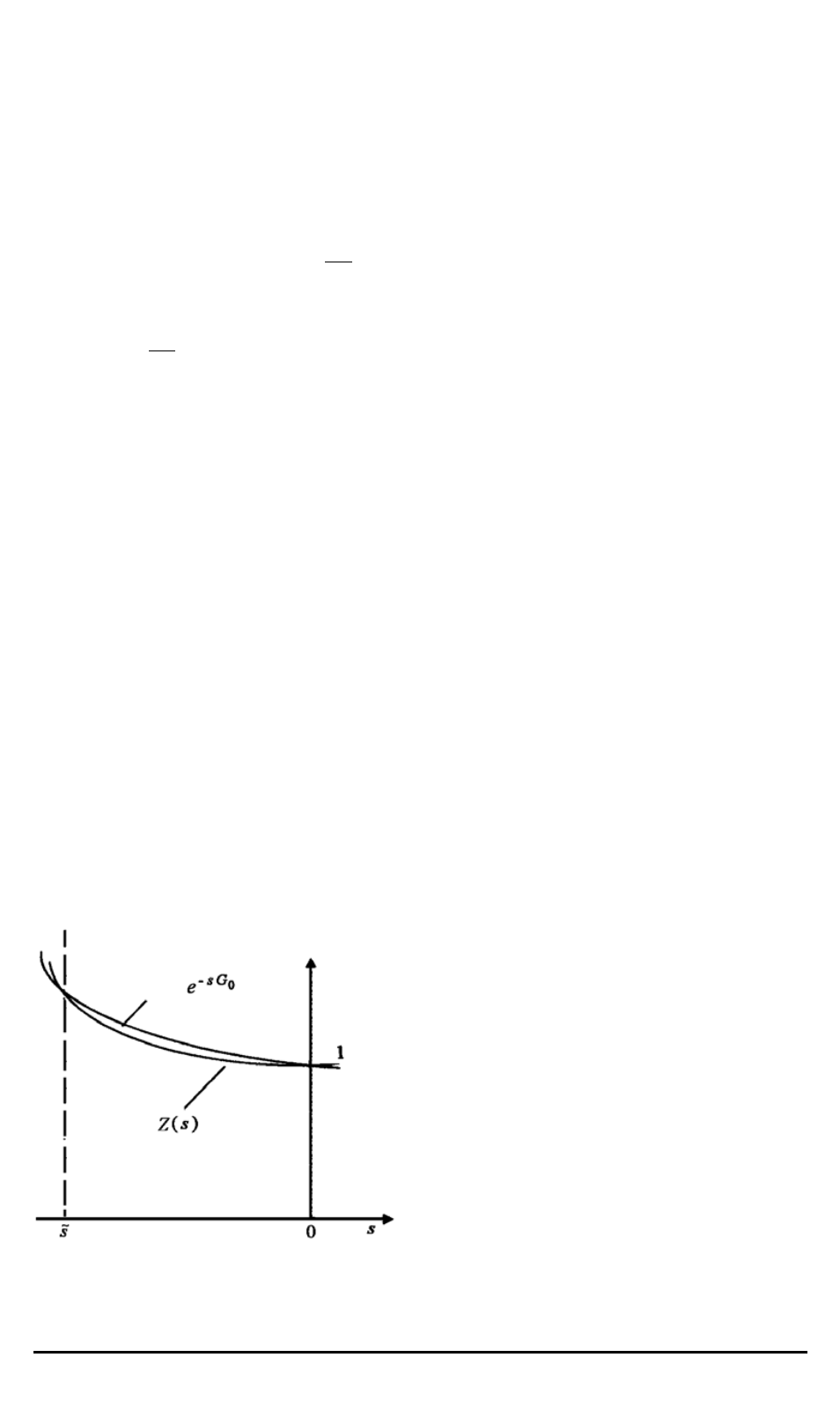
Следовательно, во-первых, при малых по модулю отрицательных зна-
чениях
s
имеем неравенство (см. рисунок)
e
−
sG
0
> Z
(
s
)
,
(21)
Решение характеристического урав-
нения (16)
где
Z
(
s
) =
Y
min
0
e
−
sy
dF
Y
(
y
)
, во-
вторых, производные левой и пра-
вой частей уравнения(16) в точке
s
= 0
отличны между собой, а от-
сюда следует, что корень
s
= 0
—
простой.
Далее предположим, что на
страховую плату наложено ограни-
чение вида
G
0
+
a < Y
min
,
(22)
где
a
— некотораяположительная
константа.
84
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2005. № 4


