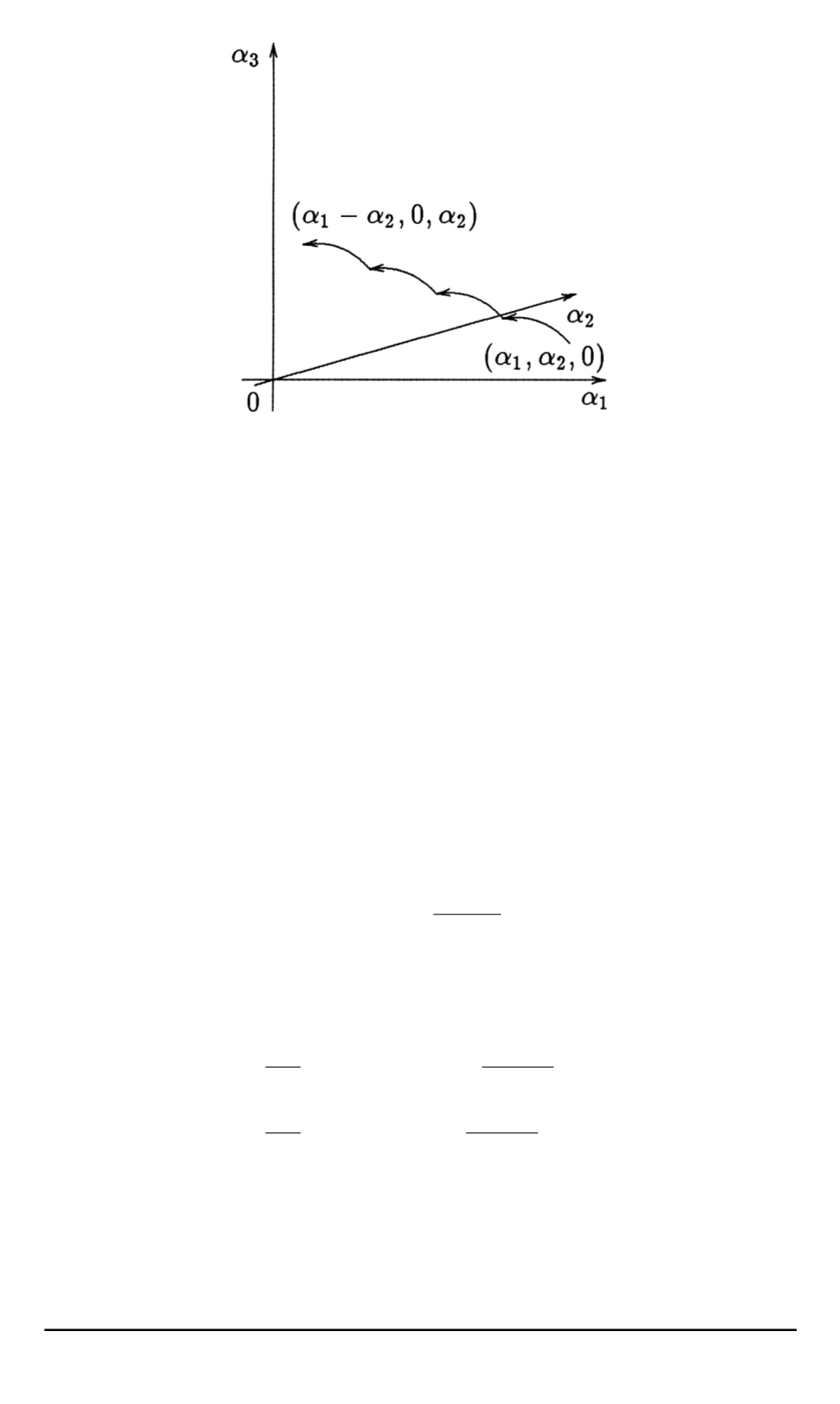
Рис. 3. Реализация процесса
T
1
+
T
2
→
T
3
, случай
α
1
> α
2
(
ξ
1
(
t
)
, ξ
2
(
t
)
, ξ
3
(
t
))
при начальном состоянии
(
α
1
, α
2
,
0)
изображена на
рис. 3. Если
α
1
≥
α
2
, то остановка процесса произойдет в погло-
щающем состоянии
(
α
1
−
α
2
,
0
, α
2
)
, и если
α
2
≥
α
1
, то в состоянии
(0
, α
2
−
α
1
, α
1
)
.
Марковский процесс
(
ξ
1
(
t
)
, ξ
2
(
t
)
, ξ
3
(
t
))
представляет собой модель
химической реакции
T
1
+
T
2
→
T
3
[2]. Состояние процесса
(
α
1
, α
2
, α
3
)
интерпретируется как наличие
α
1
элементов типа
T
1
,
α
2
элементов
типа
T
2
,
α
3
элементов типа
T
3
; в случайные моменты времени пары
элементов
T
1
+
T
2
превращаются в элемент типа
T
3
. В работе [2] об-
суждается связь второго уравнения (29) и известного в химической
кинетике закона действующих масс [7], [21]; там же получены гро-
моздкие явные выражения для переходных вероятностей процесса.
С помощью экспоненциальной производящей функции
F
(
t
;
z
1
, z
2
;
s
1
, s
2
, s
3
) =
∞
X
α
1
,α
2
=0
z
α
1
1
z
α
2
2
α
1
!
α
2
!
F
(
α
1
,α
2
,
0)
(
t
;
s
1
, s
2
, s
3
)
,
первая и вторая системы дифференциальных уравнений Колмогорова
для рассматриваемого процесса записываются в виде
∂
F
∂t
=
λz
1
z
2
s
3
F −
∂
2
F
∂z
1
∂z
2
,
(30)
∂
F
∂t
=
λ
(
s
3
−
s
1
s
2
)
∂
2
F
∂s
1
∂s
2
,
(31)
с начальным условием
F
(0;
z
1
, z
2
;
s
1
, s
2
, s
3
) =
e
z
1
s
1
+
z
2
s
2
.
Теорема 3.
Пусть марковский процесс на множестве состояний
N
3
задан плотностями переходных вероятностей
(28).
Двойная про-
изводящая функция переходных вероятностей имеет вид
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2007. № 2
57


