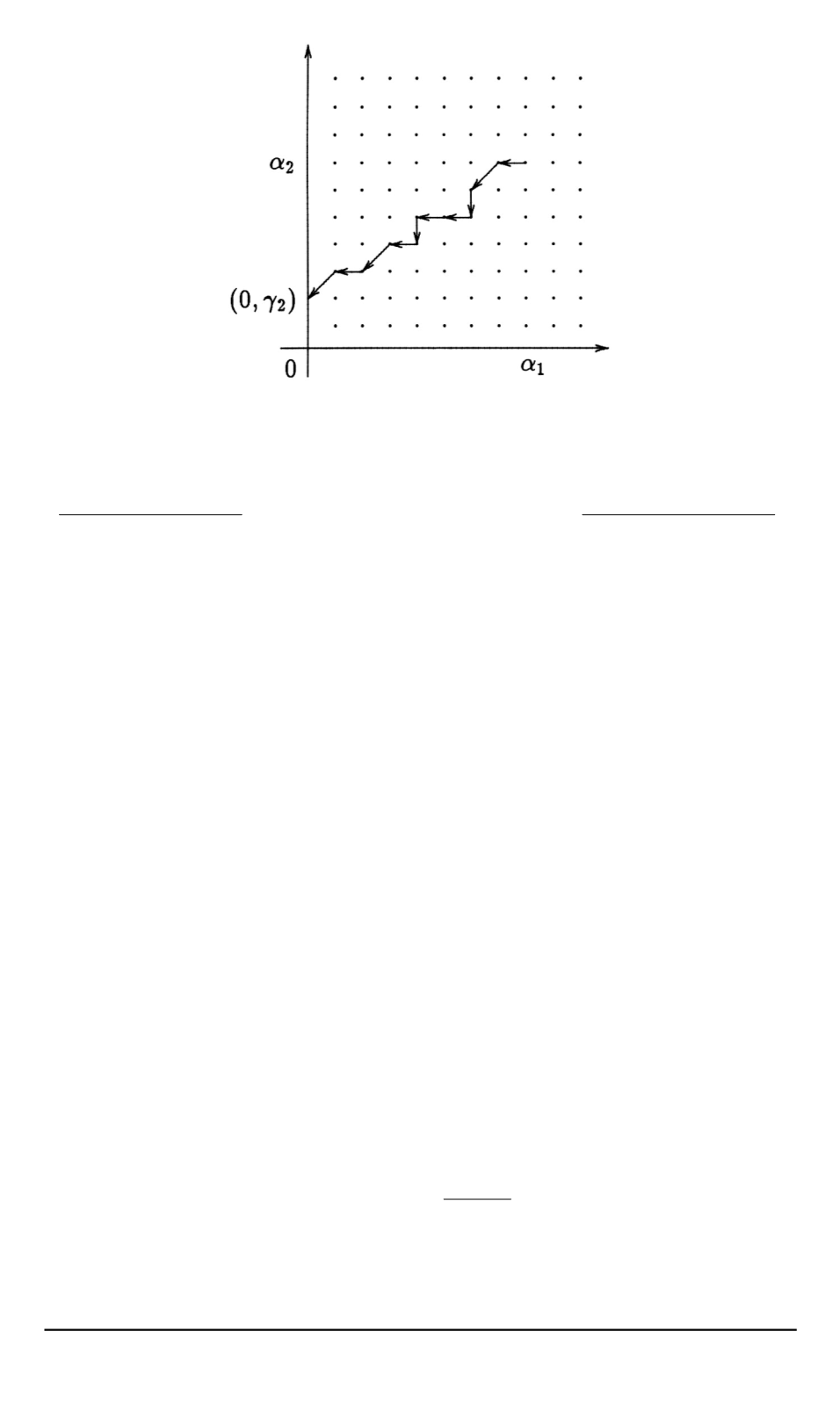
Рис. 2. Реализация двухмерного процесса гибели
нения в частных производных [21]
∂F
(
α
1
,α
2
)
(
t
;
s
1
, s
2
)
∂t
=
λ
(
p
00
+
p
10
s
1
+
p
01
s
2
−
s
1
s
2
)
∂
2
F
(
α
1
,α
2
)
(
t
;
s
1
, s
2
)
∂s
1
∂s
2
,
с начальным условием
F
(
α
1
,α
2
)
(0;
s
1
, s
2
) =
s
α
1
1
s
α
2
2
.
Пример реализации процесса
(
ξ
1
(
t
)
, ξ
2
(
t
))
изображен на рис. 2. В
начальном состоянии
(
α
1
, α
2
)
марковский процесс находится случай-
ное время
τ
(
α
1
,α
2
)
,
P
{
τ
(
α
1
,α
2
)
≤
t
}
= 1
−
e
−
α
1
α
2
λt
. Затем с вероятностью
p
10
процесс переходит в состояние
(
α
1
, α
2
−
1)
, с вероятностью
p
00
переходит в состояние
(
α
1
−
1
, α
2
−
1)
или с вероятностью
p
01
перехо-
дит в состояние
(
α
1
−
1
, α
2
)
. Далее получим аналогичную эволюцию
случайного процесса. Состояния
{
(
γ
1
,
0)
,
(0
, γ
2
)
, γ
1
, γ
2
= 0
,
1
,
2
, . . .
}
являются поглощающими. “Вложенная цепь Маркова” для процесса
(
ξ
1
(
t
)
, ξ
2
(
t
))
является случайным блужданием на
N
2
.
Марковский процесс
(
ξ
1
(
t
)
, ξ
2
(
t
))
представляет собой модель по-
пуляции с особями мужского рода и особями женского рода. Состоя-
ние
(
α
1
, α
2
)
интерпретируется как наличие совокупности из
α
1
особей
типа
T
1
и
α
2
особей типа
T
2
; в случайные моменты времени происхо-
дят взаимодействия пар различных особей, превращающихся в новые
совокупности особей. Основные предположения в модели: любая па-
ра особей
T
1
+
T
2
в популяции порождает потомство независимо от
всех других; частота актов порождения новых особей пропорциональ-
на числу особей типа
T
1
и пропорциональна числу особей типа
T
2
.
С помощью экспоненциальной производящей функции
F
(
t
;
z
1
, z
2
;
s
1
, s
2
) =
∞
X
α
1
,α
2
=0
z
α
1
1
z
α
2
2
α
1
!
α
2
!
F
(
α
1
,α
2
)
(
t
;
s
1
, s
2
)
первая и вторая системы дифференциальных уравнений для пере-
ходных вероятностей такого марковского процесса записываются
52
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2007. № 2


