Покажем, что
lim
c
→
+
∞
t
k
Z
0
[
Q
1
(
b
(
t
) +
c d
(
t
))
Q
2
(
b
(
t
) +
c d
(
t
)) +
Q
3
(
b
(
t
) +
c d
(
t
))]
dt
= +
∞
.
(31)
Представим интеграл в виде суммы
t
k
Z
0
[
Q
1
(
b
(
t
) +
c d
(
t
))
Q
2
(
b
(
t
) +
c d
(
t
)) +
Q
3
(
b
(
t
) +
c d
(
t
))]
dt
=
=
t
k
Z
0
Q
1
(
b
(
t
) +
c d
(
t
))
Q
2
(
b
(
t
) +
c d
(
t
))
dt
+
t
k
Z
0
Q
3
(
b
(
t
) +
c d
(
t
))
dt.
(32)
Рассмотрим сначала интеграл, содержащий произведение функций
Q
1
и
Q
2
.
По условию функция
Q
2
(
z
)
удовлетворяет условию (27), поэтому
8
c
8
t
2
[0
, t
k
] : 0
< N
1
≤
Q
2
(
b
(
t
) +
c d
(
t
))
≤
N
2
.
(33)
Функция
b
(
t
)
, как непрерывная функция
t
, достигает на отрезке
[0
, t
k
]
наибольшего и наименьшего значений. Обозначим их через
b
max
и
b
min
.
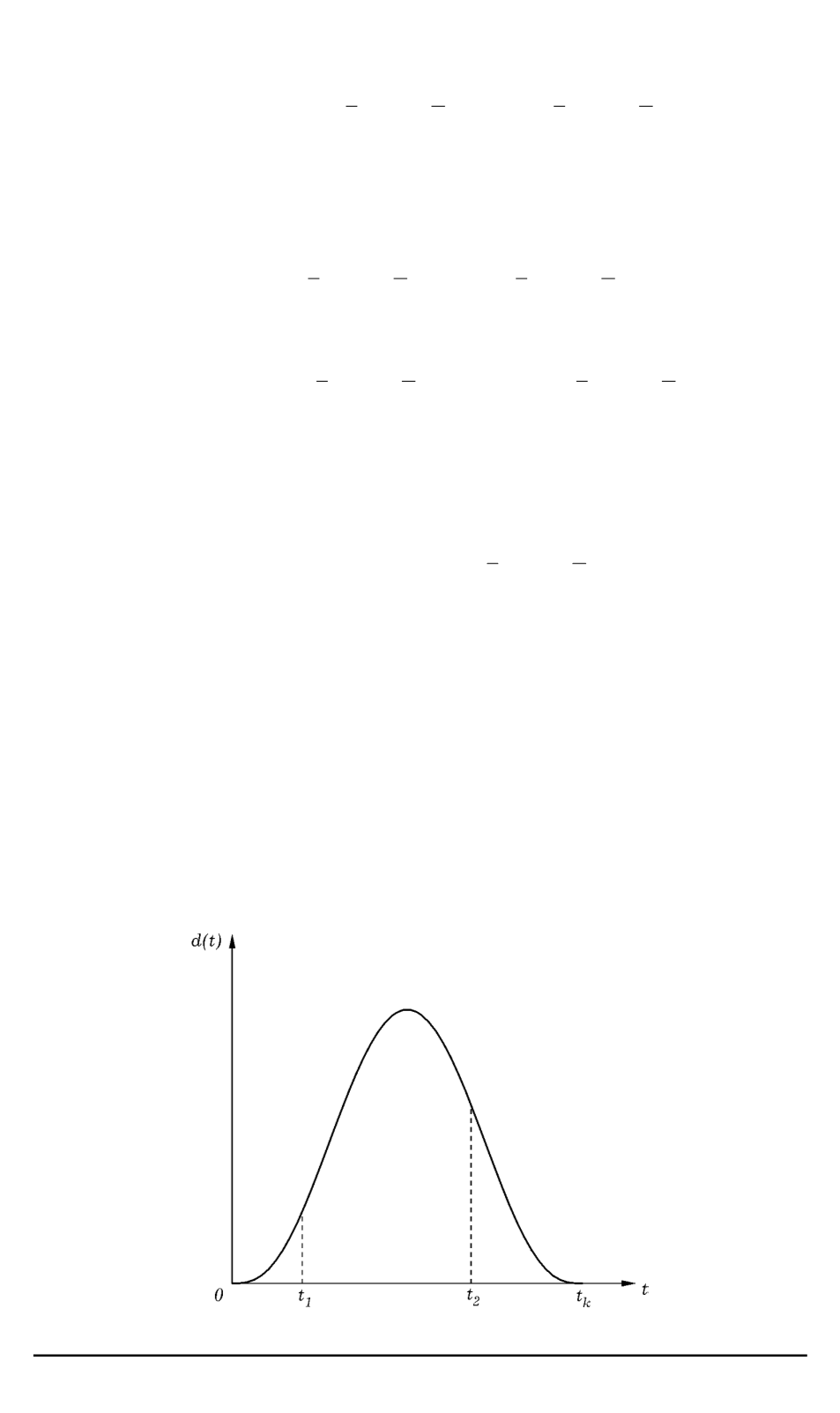
Возьмем произвольные значения
t
1
,
t
2
, принадлежащие интервалу
(0
, t
k
)
, так что
0
< t
1
< t
2
< t
k
(рис. 1). На отрезке
[
t
1
, t
2
]
функция
d
(
t
)
достигает своего наименьшего значения
d
min
, причем
d
min
>
0
.
По условию теоремы
lim
z
1
→
+
∞
Q
1
(
z
1
) = +
∞ , 8
>
0
9
δ >
0
8
z
1
:
z
1
> δ
)
Q
1
(
z
1
)
> .
Рис. 1. Функция
d
(
t
)
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2006. № 3
19


