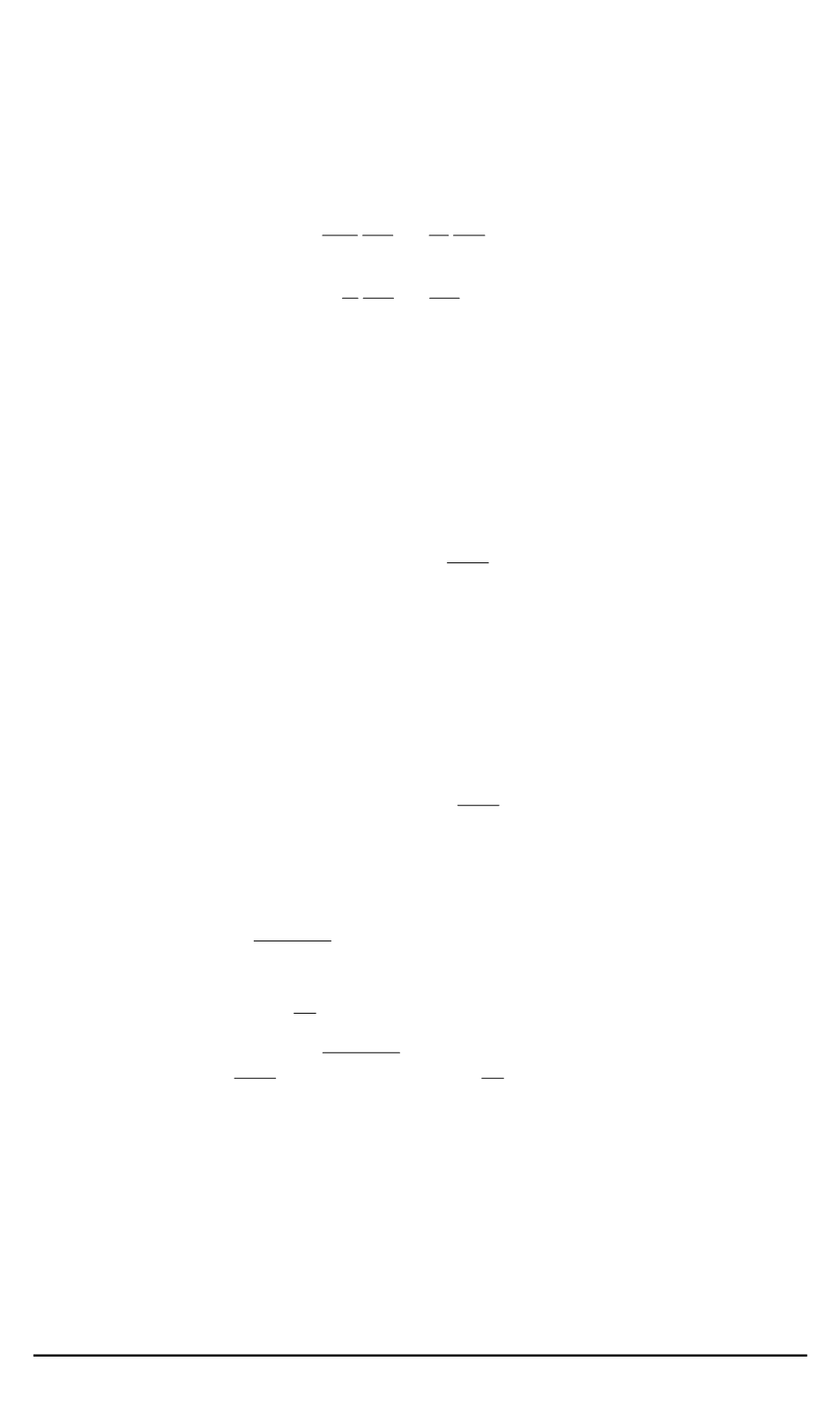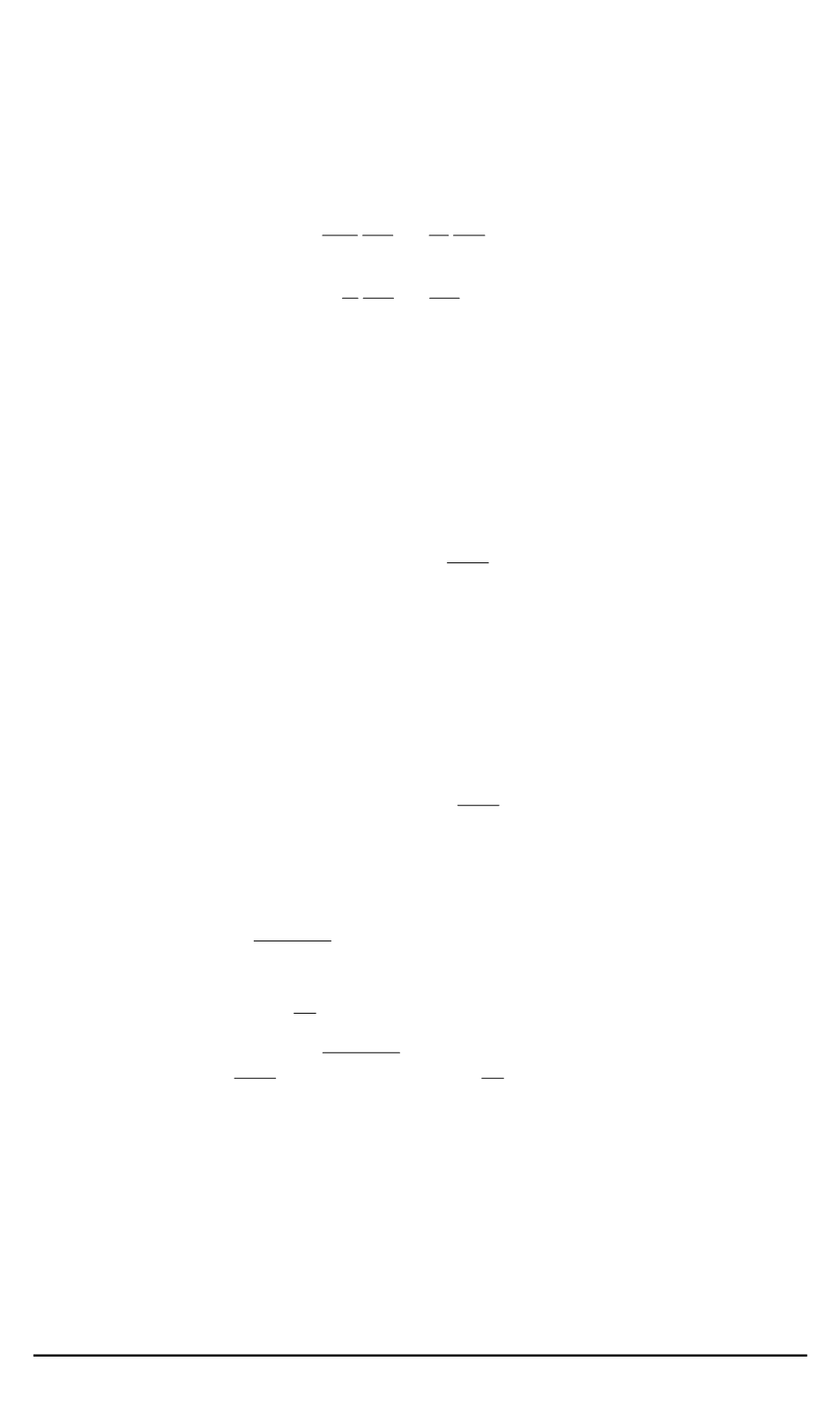
Уравнения для функций
φ
, которые следует взять в качестве ко-
ординатных для преобразования системы (11) к квазиканоническому
виду (13), имеют следующий вид:
B
1
φ
= 0
, B
2
φ
= 0
,
т. е.
1
mv
∂φ
∂β
+
l
f
J
∂φ
∂ω
= 0;
−
β
v
∂φ
∂β
+
∂φ
∂v
= 0
.
(14)
Поскольку распределение
H
0
инволютивно и регулярно при
v
6
= 0
,
то система (14) линейных уравнений в частных производных имеeт
четыре первых функционально независимых интеграла. Первые три
можно выбрать так:
φ
1
=
x
,
φ
2
=
y
,
φ
3
=
ψ
, поскольку ни в одном
уравнении системы нет производных по этим переменным.
Решив систему (14), получим четвертый первый интеграл в виде
φ
4
=
vβ
−
J
ml
f
ω.
В результате имеем, что для преобразования систему (11) к виду
(13) необходимо использовать замену переменных:
z
1
=
x, z
2
=
L
A
x
=
v
cos(
β
+
ψ
);
z
3
=
y, z
4
=
L
A
y
=
v
sin(
β
+
ψ
)
,
η
1
=
ψ, η
2
=
vβ
−
J
ml
f
ω.
(15)
Обратная подстановка имеет вид
x
=
z
1
, y
=
z
3
, ψ
=
η
1
;
v
=
p
z
2
2
+
z
2
4
;
β
= arctg
z
4
z
2
−
η
1
;
ω
=
ml
f
J
q
z
2
2
+
z
2
4
arctg
z
4
z
2
−
η
1
−
η
2
.
(16)
Отметим, что ограничение
z
2
6
= 0
не является существенным, по-
скольку вместо функции
arctg
z
можно использовать функцию двух
переменных
atan2(
z
4
, z
2
)
, определенную при всех значениях аргумен-
тов.
Для синтеза управлений нет необходимости записывать систему
(11) в специальном квазиканоническом виде (13) относительно пе-
ременных
z, η
, поскольку эта система предназначена для получения
40
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2008. № 2